If the current supplied to a variable resistor is constant, draw a graph between voltage and resistance
To solve the problem of drawing a graph between voltage (V) and resistance (R) when the current (I) supplied to a variable resistor is constant, we can follow these steps:
1. Understand Ohm's Law:
According to Ohm's Law, the relationship between voltage (V), current (I), and resistance (R) is given by the formula:
V=I×R
Here, V is the voltage across the resistor, I is the current flowing through it, and R is the resistance.
2. Identify the Constants:
Since the problem states that the current (I) is constant, we can denote this constant current as I0. Thus, the equation can be rewritten as:
V=I0×R
3. Establish the Relationship:
From the equation V=I0×R, we can see that voltage (V) is directly proportional to resistance (R) when the current (I) is constant. This means that as resistance increases, voltage also increases linearly.
4. Draw the Graph:
- On the graph, place Voltage (V) on the y-axis and Resistance (R) on the x-axis.
- Since V is directly proportional to R, the graph will be a straight line starting from the origin (0,0) and sloping upwards. The slope of the line will be equal to the constant current I0.
5. Label the Graph:
- Clearly label the axes: y-axis as Voltage (V) and x-axis as Resistance (R).
- Indicate that the line represents the relationship V=I0×R.
Final Graph:
The graph will look like a straight line passing through the origin, indicating that as resistance increases, voltage increases linearly.
According to Ohm's Law, the relationship between voltage (V), current (I), and resistance (R) is given by the formula:
V=I×R
Here, V is the voltage across the resistor, I is the current flowing through it, and R is the resistance.
Since the problem states that the current (I) is constant, we can denote this constant current as I0. Thus, the equation can be rewritten as:
V=I0×R
From the equation V=I0×R, we can see that voltage (V) is directly proportional to resistance (R) when the current (I) is constant. This means that as resistance increases, voltage also increases linearly.
- On the graph, place Voltage (V) on the y-axis and Resistance (R) on the x-axis.
- Since V is directly proportional to R, the graph will be a straight line starting from the origin (0,0) and sloping upwards. The slope of the line will be equal to the constant current I0.
- Clearly label the axes: y-axis as Voltage (V) and x-axis as Resistance (R).
- Indicate that the line represents the relationship V=I0×R.
The graph will look like a straight line passing through the origin, indicating that as resistance increases, voltage increases linearly.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Conceptual Problems3videos
CURRENT ELECTRICITY
- BOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Very short Q/A7videos
CURRENT ELECTRICITY
- BOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-29videos
COMMUNICATION SYSTEMS
- BOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise191videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
.A cell of emf E and internal resistance r is connected across a variable resistor. Plot a graph showing variation of terminal voltage V of cell versus the current.
View SolutionThe current-voltage graph for a resistor is as shown in the figure. Is it right to say that resistance decreases as the current through it increases ?
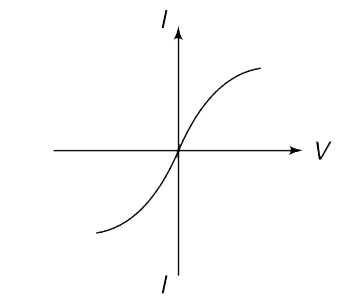 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A fixed resistor is cannected in parallel with a variable resistor, both are connected to a real battery (internal resistance is not negligible). Originally the fixed and variable resistors have the same resistance
As the resistance of the variable resistor is decreased, the current through the fixed resistorAincreasesBdecreasesCremains the sameDcannot be determined without more information - Question 2 - Select One
A fixed resistor is cannected in parallel with a variable resistor, both are connected to a real battery (internal resistance is not negligible). Originally the fixed and variable resistors have the same resistance
If the resistance of the variable resistor is decreased slightly, the rate at which energy is transferred to the variable resistorAincreasesBdecreasesCremains the sameDcannot be determined without more information - Question 3 - Select One
A fixed resistor is cannected in parallel with a variable resistor, both are connected to a real battery (internal resistance is not negligible). Originally the fixed and variable resistors have the same resistance
As the resistance of the variable resistor is decreased, the rate at which energy is trausferred to the fixed resistorAincreasesBdecreasesCremains the sameDcannot be determined without more information
The values of current I flowing in a given resistor for the corresponding values of potential difference V across the resistor are given below:

Plot a graph between V and I and calculate the resistance of that resistor,View SolutionThe voltage stabilizer S is a device whose idealized characteristic is depicted in Fig. 26.21. The voltage stabilizer is connected in series with a normal resistor R to the power supply whose e.m.f. is ε. Neglecting the internal resistance of the power supply find the current in the circuit and the voltage drop across the voltage stabilizer and the resistor.
 View Solution
View SolutionA power supply of fixed emf E is connected to a variable resistor (resistance = R) and an ammeter of resistance RA. The internal resistance of supply is r. The potential difference between the terminals of the power supply in closed circuits is denoted by V and current in circuit denoted by I. A graph is obtained between V and I by drawing varying amount of current from the supply. The correct V−I graph for the given situation is
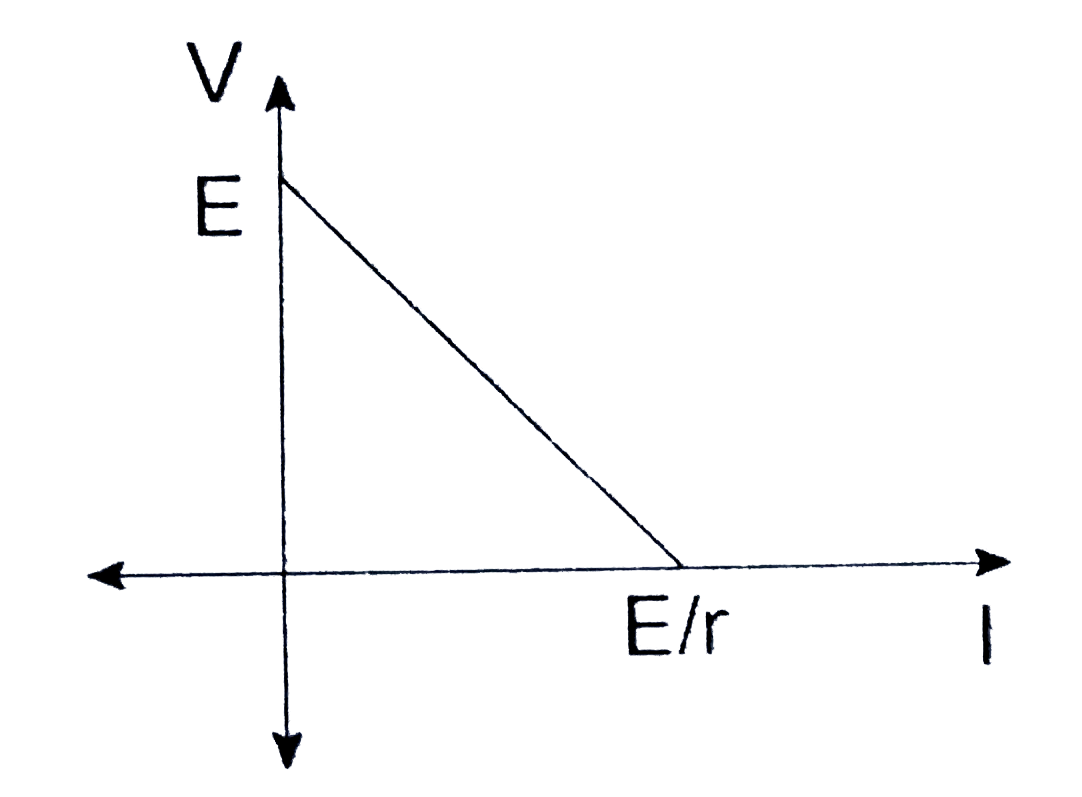
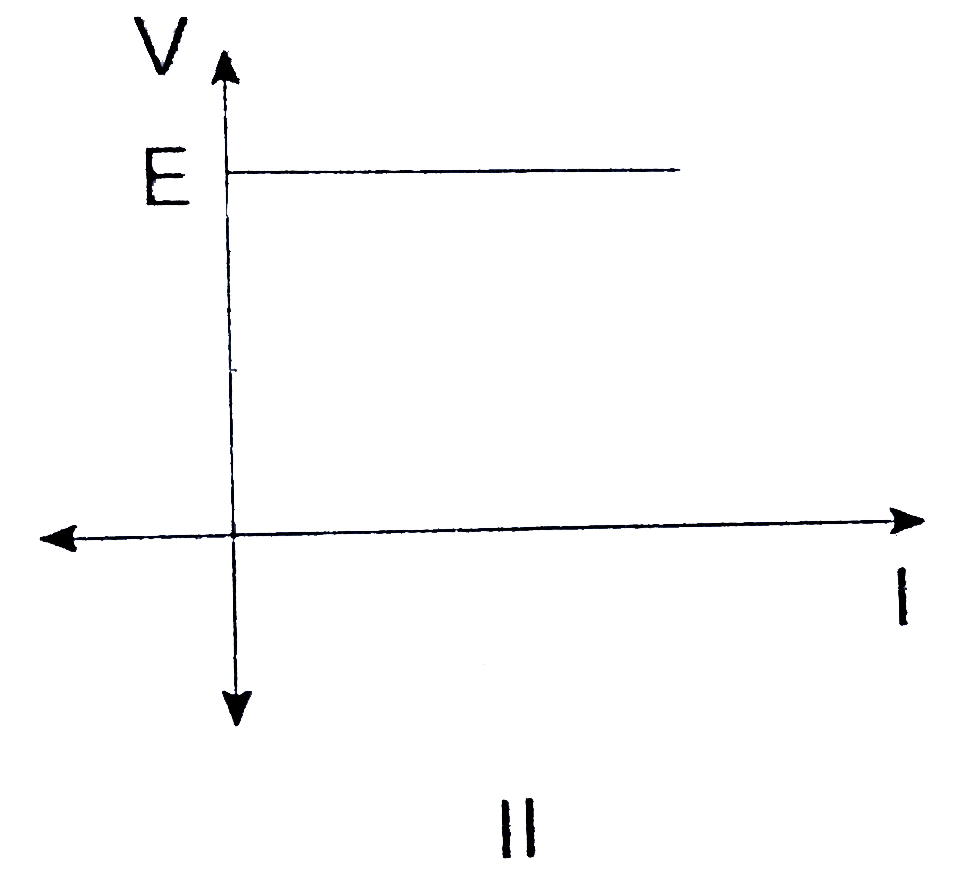
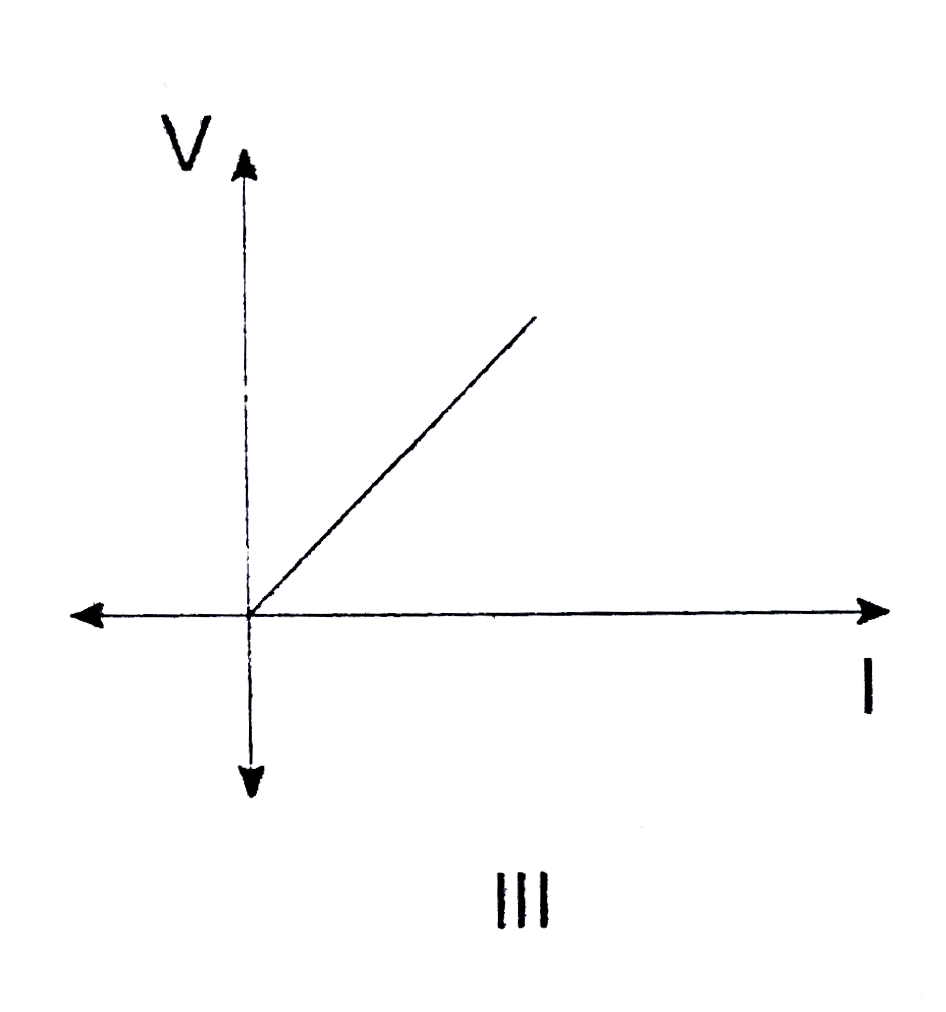
 View Solution
View SolutionDifferent voltages are applied across a P−N junction and the currents are measured for each value. Which of the following graphs is obtained between voltage and current?
View SolutionHeat is produced at a rate given by H in a resistor when it is connected across a supply of voltage V. If now the resistance of the resistor is doubled and the supply voltage is made V/3 then the production of heat in the resistor will be
View Solution

