State and prove Wheat stone bridge principle. Discuss the determinaton of unknown temperature with its help.
Step-by-Step Solution
Step 1: State the Wheatstone Bridge Principle
The Wheatstone Bridge principle states that a circuit is balanced when the ratio of the resistances in one branch is equal to the ratio of the resistances in the other branch. Mathematically, for a balanced Wheatstone Bridge, the following condition holds:
R1R2=R3R4
Where:
- R1 and R2 are the resistances in one branch.
- R3 and R4 are the resistances in the other branch.
Step 2: Prove the Wheatstone Bridge Principle
1. Circuit Setup: Consider a Wheatstone Bridge circuit consisting of four resistors R1,R2,R3, and R4 arranged in a diamond shape with a galvanometer G connected between the midpoints of the two branches.
2. Balanced Condition: When the bridge is balanced, there is no current flowing through the galvanometer. This implies that the potential difference across the galvanometer is zero.
3. Applying Ohm's Law: According to Ohm's law, the potential difference across a resistor is given by V=I⋅R. In the balanced condition:
- The potential drop across R1 is equal to the potential drop across R3.
- The potential drop across R2 is equal to the potential drop across R4.
4. Setting Up Equations:
- For the upper branch: V−V1=I1R1 and V1=I2R2
- For the lower branch: V1=I3R3 and V−V1=I4R4
5. Equating Currents: Since no current flows through the galvanometer, we can equate the ratios:
I1I2=R2R1andI3I4=R4R3
6. Final Condition: Since I1=I3 and I2=I4, we can derive:
R1R2=R3R4
Thus, the Wheatstone Bridge is balanced when this condition holds true.
Step 3: Determination of Unknown Temperature Using Wheatstone Bridge
1. Resistance and Temperature Relation: The resistance of a conductor changes with temperature according to the formula:
R=R0(1+αΔT)
Where:
- R0 is the resistance at a reference temperature.
- α is the temperature coefficient of resistance.
- ΔT is the change in temperature.
2. Setting Up the Bridge: In a Wheatstone Bridge, if we know three resistances R1,R3, and R4, we can find the unknown resistance R2 at a certain temperature.
3. Calculating Unknown Resistance: Rearranging the balanced Wheatstone Bridge condition:
R2=R1R4R3
4. Finding Unknown Temperature: If we measure R2 at a new temperature T, we can substitute into the resistance-temperature relation:
R2=R0(1+α(T−T0))
Where T0 is the reference temperature.
5. Solving for Temperature: Rearranging gives:
T=T0+R2−R0R0α
This allows us to calculate the unknown temperature based on the measured resistance.
- R1 and R2 are the resistances in one branch.
- R3 and R4 are the resistances in the other branch.
- The potential drop across R1 is equal to the potential drop across R3.
- The potential drop across R2 is equal to the potential drop across R4.
- For the upper branch: V−V1=I1R1 and V1=I2R2
- For the lower branch: V1=I3R3 and V−V1=I4R4
I1I2=R2R1andI3I4=R4R3
R1R2=R3R4
R=R0(1+αΔT)
Where:
- R0 is the resistance at a reference temperature.
- α is the temperature coefficient of resistance.
- ΔT is the change in temperature.
R2=R1R4R3
R2=R0(1+α(T−T0))
Where T0 is the reference temperature.
T=T0+R2−R0R0α
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Conceptual Problems
3 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Very short Q/A
7 Videos
- COMMUNICATION SYSTEMSBOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-2
9 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise
191 Videos
Similar Questions
Knowledge Check
In a practical wheat stone bridge circuit as shown, when one more resistance of 100Ω is connected in parallel with unknown resistance 'x', then ratio l1/l2 become '2'l1 is balance length , AB is a uniform wire. Then value of 'x' must be :
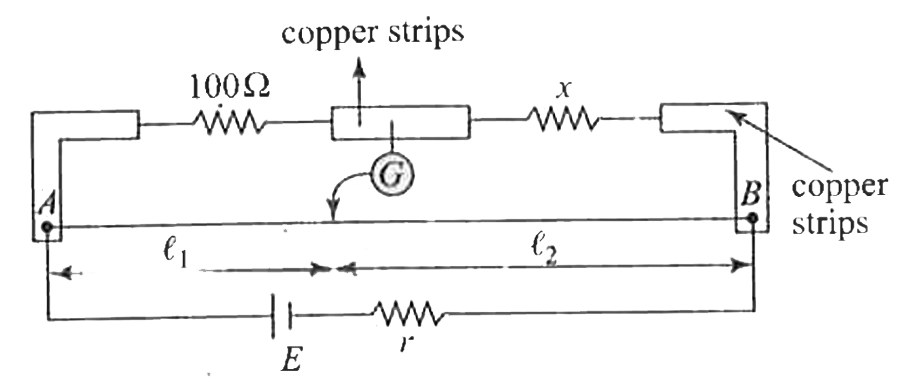 A50ΩB100ΩC200ΩD400Ω
A50ΩB100ΩC200ΩD400Ω
State and prove the principle of conservation of linear momentum Show that a gun recoils when a bullet is fired from it
View SolutionExplain the principle of working of a meter bridge. Draw the circuit diagram for determination of an unknown resistance using it.
View SolutionLaw of conservation of angular momentum
View SolutionState Archimedes's Principle. Describe an experiment for its verification.
View SolutionWith the help of a circuit diagram, explain the working principle of a metre bridge. How is it used to determine the unknown resistance of a given wire? Write the necessary precautions to minimise the error in the result?
View SolutionWrite the names of the important ores of aluminium. Discuss the principle of extraction of metal from its ore.
View SolutionWith the help of a circuit diagram, explain the working principle of metre bridge. How is it used to determine the unknown resistance of a given wire ? Write the necessary precautions to minimise error in the result.
View Solution
