Find the acceleration of the body of mass m2 in the arrangement shown in figure. If the massm2 is η time great as the mass m1 and the angle that the inclined plane forms with the horizontal is equal to θ. The masses of the pulley and threads, as well as the friction, are assumed to be negligible.
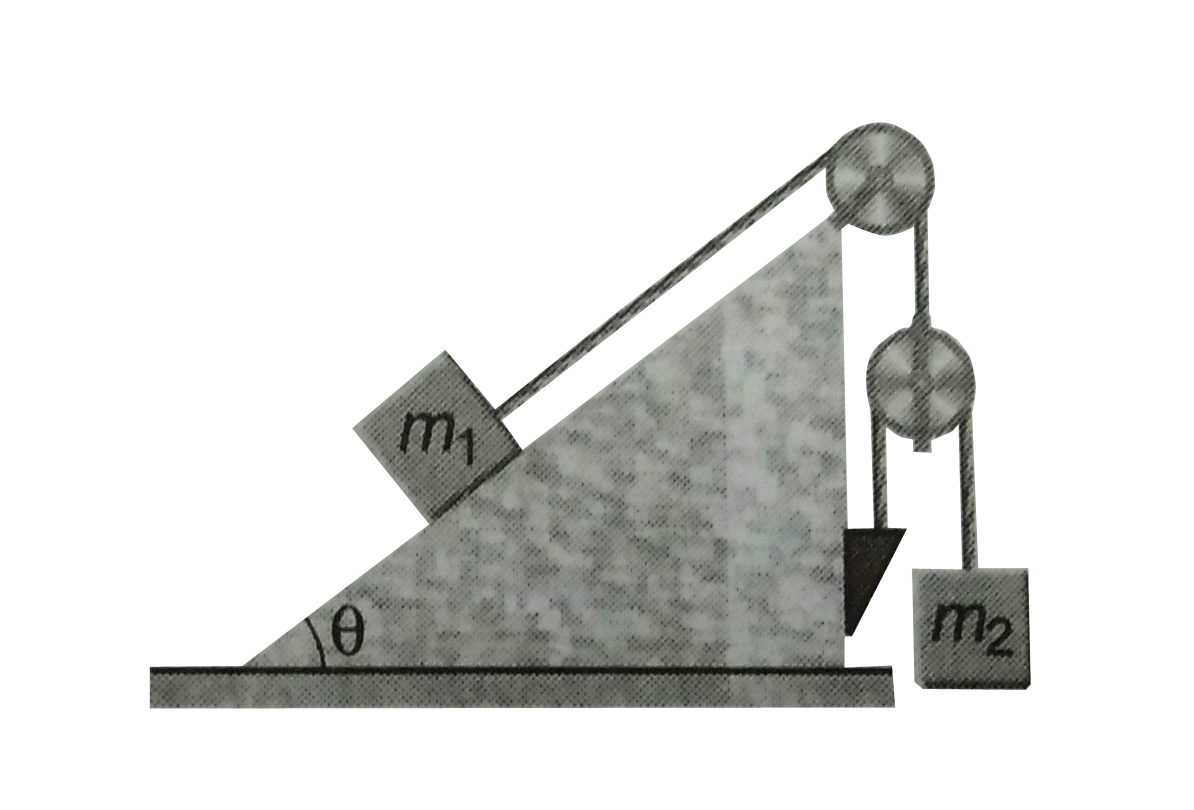
Let us write Newton's second law for both, bar 1 and body 2 in terms of projection having taken the positive direction of x1 and x2 as shown in the figure and assuming that body 2 starts sliding, say, upward along the incline
T1−m1gsinα=m1w1 (1)
m2g−T2=m2w (2)
For the pulley, moving in vertical direction from the equation Fx=mwx
2T2−T1=(mP)w1=0
(as mass of the pulley mP=0)
or T1=2T2 (3)
As the length of the threads are constant, the kinematical relationship of accelerations becomes
w=2w1 (4)
Simultaneous solutions of all these equations yields:
w=2g(2m2m1−sinα)(4m2m1+1)=2g(2η−sinα)(4η+1)
As η>1, w is directed vertically downward, and hence in vector from
→w=2→g(2η−sinα)4η+1

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Laws Of Conservation Of Energy, Momentum And Angular Momentum
82 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation
34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
Find the acceleration of the prism of mass M and that of the bar of mass m shown in figure.
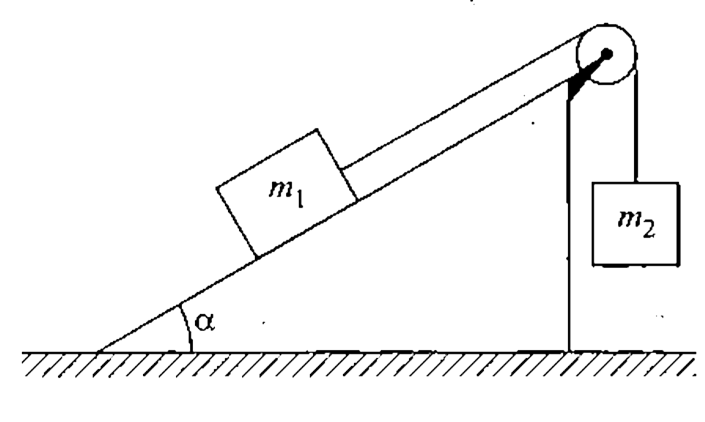
View SolutionFind the acceleration of the block of mass m in the arrangement shown in the following figures. The masses of the pulleys and the threads, as well as the friction are assumed to be negligible.

View Solution
Knowledge Check
Find the acceleration of the body of mass m2 in the arrangement shown in figure. If the massm2 is η time great as the mass m1 and the angle that the inclined plane forms with the horizontal is equal to θ. The masses of the pulley and threads, as well as the friction, are accumed to be negligible.
 Ag(2η−sinθ)4η+1B2g(η−sinθ)4η+1C2g(2η−sinθ)η+1D2g(2η−sinθ)4η+1
Ag(2η−sinθ)4η+1B2g(η−sinθ)4η+1C2g(2η−sinθ)η+1D2g(2η−sinθ)4η+1
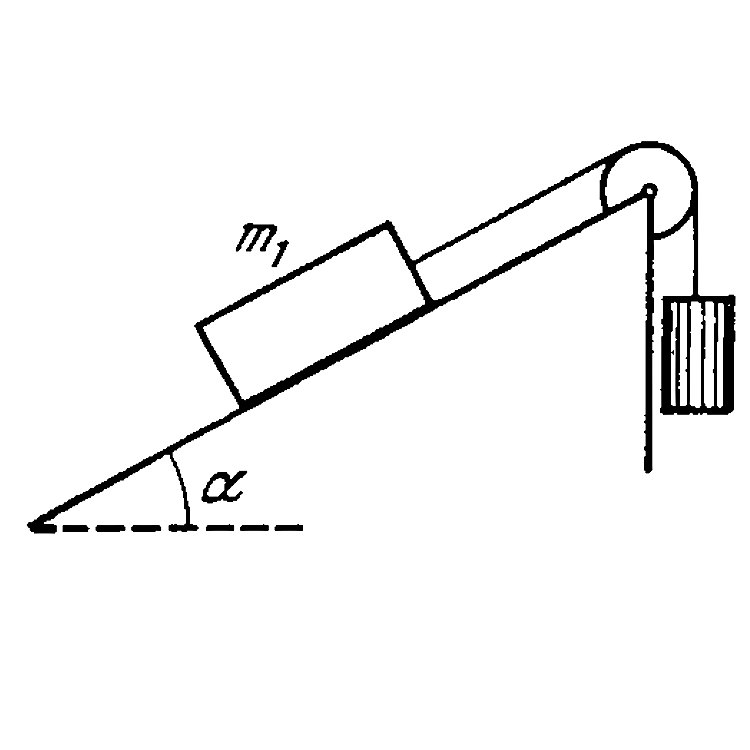
The following parameters of the arrangement of figure are available: the angle α which the inclined plane forms with the horizontal, and the coefficient of friction k between the body m1 and the inclined plane. The masses of the pulley and the threads, as well as the friction in the pulley, are negligible. Assuming both bodies to be motionless at the initial moment, find the mass ratio m2/m1 at which the body m2
(a) starts coming down,
(b) starts going up,
(c) is at rest.
View SolutionFind the accelerations of rod A and wedge B in the arrangement shown in figure if the ratio of the mass of the wedge to that of the rod equals η, and the friction between all contact surfaces is negligible.

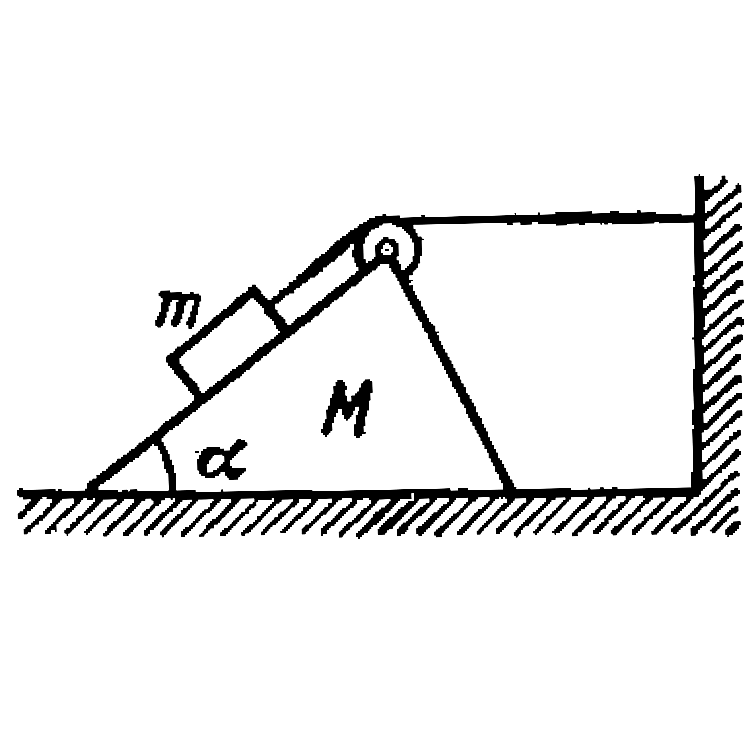
View SolutionIn the arrangement shown in figure the masses m of the bar and M of the wedge, as well as the wedge angle α, are known. The masses of the pulley and the thread are negligible. The friction is absent. Find the acceleration of the wedge M.
View SolutionFind the acceleration of rod A and wedge B in the arrangement shown in figure if the mass of rod equal that of the wedge and the friction between all contact surfaces is negligible Take angle of wedge as 45∘&g=9.8m/s2

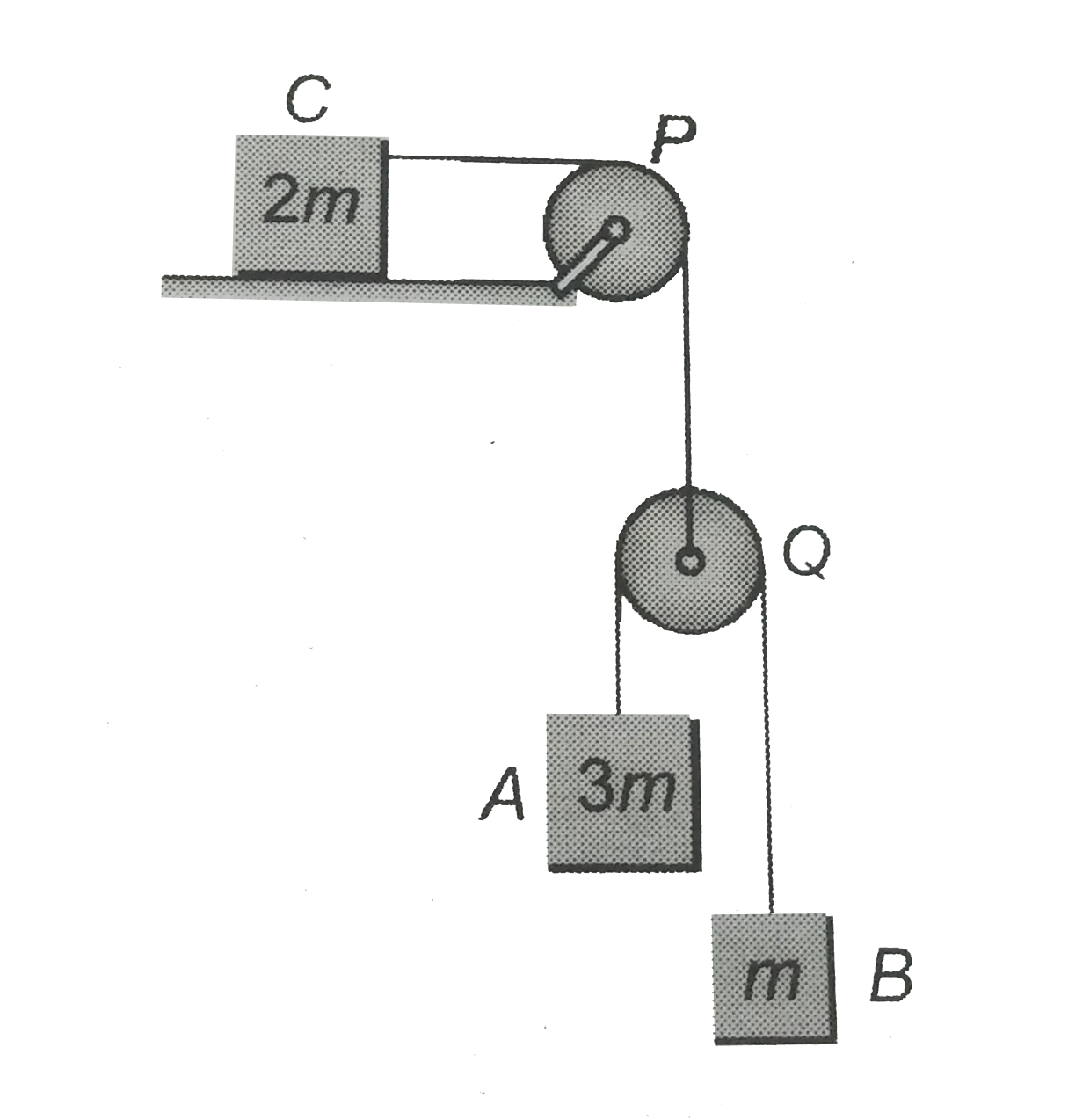
View SolutionIn the arrangement shown in the figure, the blocks have masses 3m,m and 2m, the friction is absent, the masses of the pulleys and the threads are negligible. Find the acceleration of mass 3m.
View SolutionIn terms of masses m1,m2 and g, find the acceleration of both the blocks shown in Fig. Neglect all friction and masses of the pulley.
View SolutionIn the arrangement shown in fig the bodies have masses m0,m1andm2 the friction is absent the masses of pulleys and the threads are negligible find the acceleration of the body m1

View Solution
