What work should be done in order to squeeze all water from a horizontally located cylinder (figure) during the time t by means of a constant force acting on the piston? The volume of water in the cylinder is equal to V, the cross-sectional area of the orifice to s, with s being considerably less than the piston area. The friction and viscosity are negligibly small.

Let the force acting on the piston be F and the length of the cylinder be l.
Then, work done =Fl (1)
Applying Bernoulli's theorem for points A and B, p=12ρv2 where ρ is the density and v is the velocity at point B. Now, force on the piston,
F=pA=12ρv2A (2)
where A is the cross section area of piston. Also, discharge through the orifice during time interval t=Svt and this is equal to the volume of the cylinder, i.e.,
V=Svt or v=VSt (3)
From Eq. (1), (2) and (3) work done
=12ρv2Al=12ρAV2(St)2l=12ρV3/S3t2 (as Al=V)

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Elastic Deformation Of Asolid Body
Explore 25 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
What work should be done in order to sqeeze all water from a horizontally located cylinder (figure) during the time t by means of a constant force acting on the poston? The volume of water in the cylinder is equal to V, the cross-sectional area of the orifice is s, with s being considerablu less than the piston area. The friction and viscosity are negligibly small. Density of water is ρ

View SolutionA horizontal cylinder of length l contains water. On the left a constant force F is applied on the piston and on the right there is a small hole of area a. What is the velocity of the piston? Hence, calculate the work done in emptying the vessel in time t. brgt
 given area of cylinder is A
given area of cylinder is A
View Solution
Knowledge Check
Water is filled to height h in a fixed vertical cylinder placed on horizontal surface. At time t=0 a small hole a drilled at a height h/4 from bottom of cylinder as shown. The cross section area of hole is a and the cross-section area of cylinder is A such that A>>a.

The duration of time for which water flows out of hole is.AAa√3h2gBaA√3h2gCAa√2h3gDNone of thesePassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)
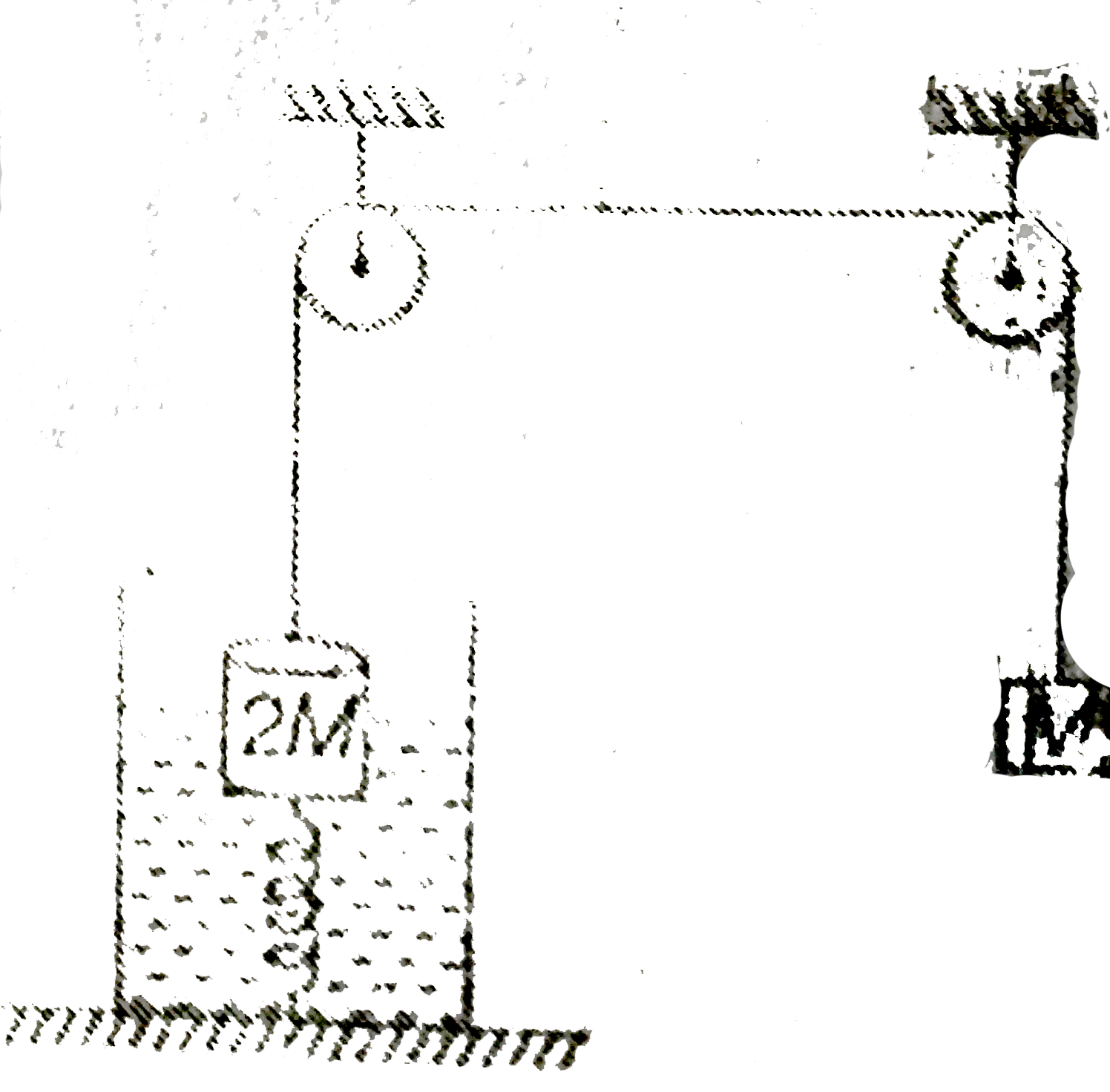
If the cylinder is pushed down from equilibrium by a distance which is half the distance as calculated in the above question, determine time period of subsequent motion.A(2pisqrt((3M)/(2(K+Arhog)B(2π√M2K+AρgC2π√3MK+AρgD2π√2MK+3AρgPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)

By what maximum distance cylinder will be pushed downward into the liquid from equilibrium position so that when it is set free then tension in the string will not vanish [Assume at equilibrium position system was at rest]A3MgK+AρgB3Mg2(K+Aρg)C8Mg3(K+Aρg)D3Mg2K+3Aρg
A flatcar of mass m0 starts moving to the right due to a constant horizontal force F(figure). Sand spills on the flatcar from a stationary hopper. The velocity of loading is constant and equal to μkg/s. Find the time dependence of the velocity and the acceleration of the flatcar in the process of loading. The friction is negligibly small.

View SolutionA horizontal cylindrical vessel with a small orifice of area s is first filled with a liquid of density ρ and then forced out through it by applying a constant force on the piston closing the cylinder. The time taken is t. The time taken is t. Calculate the work done.
View SolutionOne mole of a certain ideal gas is contained under a weight-less piston of a vertical cylinder at a temperature T. The space over the piston opens into the atmosphere. What work has to be performed on order to increase isothermally the gas volume under the piston n times by slowly raising the piston ? The friction of the piston against the cylinder walls is negligibly small.
View SolutionWater of mass m=20g is enclosed in a thermally insulated cylinder at the temperature of 0∘C under a weightless piston whose area is S=410cm2. The outside pressure is equal to standard atmospheric pressure. To what height will the piston rise when the water absorbs Q=20.0kJ of heat ?
View SolutionWater is filled to height h in a fixed vertical cylinder placed on horizontal surface. At time t=0 a small hole a drilled at a height h/4 from bottom of cylinder as shown. The cross section area of hole is a and the cross-section area of cylinder is A such that A>>a.

Let the value of horizontal distance of point where the4 water fall on horizontal surface from bottom of cylinder be x as shown. Then from time t=0 till water comes out of hole, pick the correct statement:
View Solution
