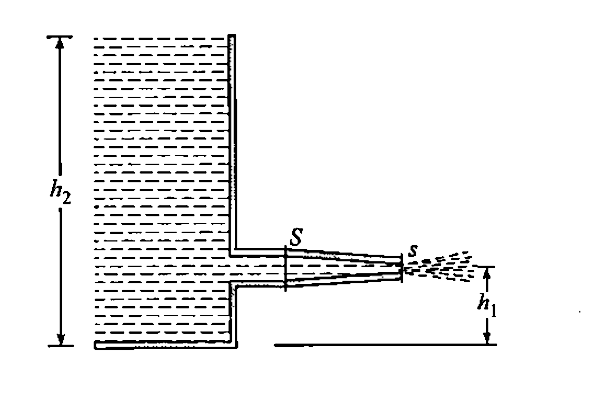
A side wall of a wide open tank is provided with a narrowing tube (figure) through which water flows out. The cross-sectional area of the tube decreases from $S = 3.0 c m^{2}$ to $s = 1.0 c m^{2}$ . The water level in the tank is $h = 4.6 m$ higher than that in the tube. Neglecting the viscosity of the water, find the horizontal component of the force tending to pull the tube out of the tank.

Text Solution

Verified by Experts

Suppose the radius at A is R and it decreases uniformly to r at B where $S = π R^{2}$ and $s = π R^{2}$ . Assume also that the semi vectical angle at 0 is $α$ . Then
$\frac{R}{L_{2}} = \frac{r}{L_{1}} = \frac{y}{x}$
So $y = r + \frac{R - r}{L_{2} - L_{1}} (x - L_{1})$
where y is the radius at the point P distant x from the vertex O. Suppose the velocity with which the liquid flows out is $V$ at A, v at B and u at P. Then by the equation of continuity
$π R^{2} V = π r^{2} v = π y^{2} u$
The velocity v of efflux is given by
$v = \sqrt{2 g h}$
and Bernoulli's theorem gives
$p_{p} + \frac{1}{2} ρ u^{2} = p_{0} + \frac{1}{2} ρ v^{2}$
where $p_{p}$ is the pressure at P and $p_{0}$ is the atmospheric pressure which is the pressure just outside of B. The force on the nozzle tending to pull it out is then
$F = \int (p_{ρ} - p_{0}) sin θ 2 π y d s$
We have subtracted $p_{0}$ which is the force due to atmospheric pressure the factor $sin θ$ gives horizontal component of the force and $d s$ is the length of the element of nozzle surface, $d s = d x sec θ$ and
$tan θ = \frac{R - r}{L_{2} - L_{1}}$
Then $F = L_{2} \int L_{1} \frac{1}{2} (v^{2} - u^{2}) ρ 2 π y \frac{R - r}{L_{2} - L_{1}} d x$
$= π ρ R \int r v^{2} (1 - \frac{r^{4}}{y^{4}}) y d y$
$= π ρ v^{2} \frac{1}{2} (R^{2} - r^{2} + \frac{r^{4}}{R^{2}} - r^{2}) = ρ g h ⎛ ⎝ \frac{π {(R^{2} - r^{2})}^{2}}{R^{2}} ⎞ ⎠$
$= ρ g h {(S - s)}^{2} / S = 6 \cdot 02 N$ on putting the values.
Note: If we try to calculate F from the momentum change of the liquid flowing out will be wrong even as regards the sign of the force.
There is of course the effect of pressure at S and s but quantitative derivation of F from Newton's law is difficult.

Updated on:21/07/2023

In the figure, the cross-sectional area of the smaller tube is a and that of the larger tube is $2 a$ . A block of mass $m$ is kept in the smaller tube having the base area that of the tube. The difference between water levels of the two tubes is

A $\frac{P_{0}}{ρ g} + \frac{m}{a ρ}$
B $\frac{P_{0}}{ρ g} + \frac{m}{2 a ρ}$
C $\frac{m}{a ρ}$
D $\frac{m}{2 ρ a}$
Water is flowing through a horizontal tube of non uniform cross-section. At a place the radius of the rube is 0.5 cm and the velocity of water there is 20 cm/s. What will be the velocity at another place wehre the radius of the tube is 1.0 cm?
A3 cm/s
B7 cm/s
C5 cm/s
D0.5 cm/s