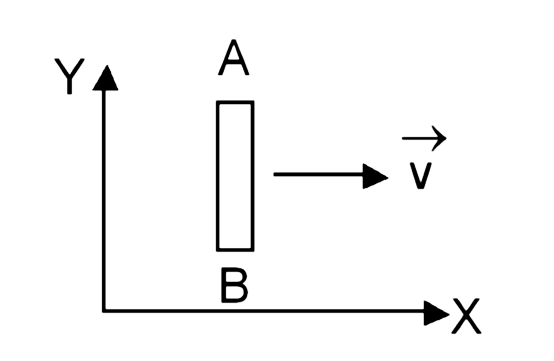
A rod AB oriented along the x axis of the reference frame K moves in the positive direction of the x axis with a constant velocity v. The point A is the forward end of the rod, and the point B its near end. Find:
(a) the proper length of the rod, if at the moment $t_{A}$ the coorniate of the point A is equal to $x_{A}$ , and at the moment $t_{B}$ the coordinate of the point B is equal to $x_{B}$ ,
(b) what time interval should separate the markings of coordinates of the rod's ends in the frame K for the difference of coordinates to become equal to the proper length of the rod.

Text Solution

Verified by Experts

(a) In the reference frame K with respect to which the rod is moving with velocity v, the coordinates of A and B are
$A : t, x_{A} + v (t - t_{A}), 0, 0$
$B : t, x_{B} + v (t - t_{B}), 0, 0$
Thus $l = x_{A} - x_{B} - v (t_{A} - t_{B}) = l_{0} \sqrt{1 - β^{2}}$
So $l_{0} = \frac{x_{A} - x_{B} - v (t_{A} - t_{B})}{\sqrt{1 - v^{2} / c^{2}}}$
(b) $\pm l_{0} - v (t_{A} - t_{B}) = l = l_{0} \sqrt{1 - v^{2} / c^{2}}$
(since $x_{A} - x_{B}$ can be either $+ l_{0}$ or $- l_{0}$ .)
Thus $v (t_{A} - t_{B}) = (\pm 1 - \sqrt{1 - v^{2} / c_{2}}) l_{o}$
i.e. $t_{A} - t_{B} = \frac{l_{0}}{v} (1 - \sqrt{1 - \frac{v^{2}}{c^{2}}})$
or $t_{B} - t_{A} = \frac{l_{0}}{v} (1 + \sqrt{1 - v^{2} / c^{2}})$

Updated on:21/07/2023

A conductor rod AB moves parallel to X-axis in a uniform magnetic field, pointing in the positive Z-direction. The end A of the rod gets-

Apositively charged
Bnegatively charged
Cneutral
Dfirst positively charged and then negatively charged.
The moment of inertia of a straight thin rod of mass M and length l about an axis perpendicular to its length and passing through its one end, is
A $\frac{m l^{2}}{12}$
B $\frac{7}{48} m l^{2}$
C $\frac{13}{48} m l^{2}$
D $\frac{19}{48} m l^{2}$