The rod A′B′ moves with a constant velocity v relative to the rod AB (figure). Both rods have the same proper length l0 and at the ends of each of them clocks are mounted, which are synchronized pariwise: A with B and A′ with B′. Suppose the moment when the clock B′ gets opposite the clock A is taken for the beginning of the time count in the reference frames fixed to each of the rods. Determine:
(a) the readings of the clocks B and B′ at the moment when they are opposite each other,
(b) the same for the clocks A and A′.

At the instant the picture is taken the coordinates of A,B,A′,B′ in the rest frame of AB are
A:(0,0,0,0)
B:(0,l0,0,0)
B′:(0,0,0,0)
A′:(01−l0√1−v2/c2,0,0)
In this frame the coordinates of B′ at other times are B′:(t,vt,0,0). So B′ is opposite to B at time t(B)=l0v. In the frame in which B′, A′ is at rest the time corresponding this is by Lorentz transformation.
t0(B′)=1√1−v2c2(l0v−vl0c2)=l0v√1−v2/c2
Similarly in the rest frame of A, B, te coordinates of A at other times are
A′:(t,−l0√1−v2c2+vt,0,0)
A′ is opposite to A at time t(A)=l0v√1−v2c2
The corresponding time in the frame in which A′, B′ are at rest is
t(A′)=γt(A)=l0v

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Hydrodynamics
25 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
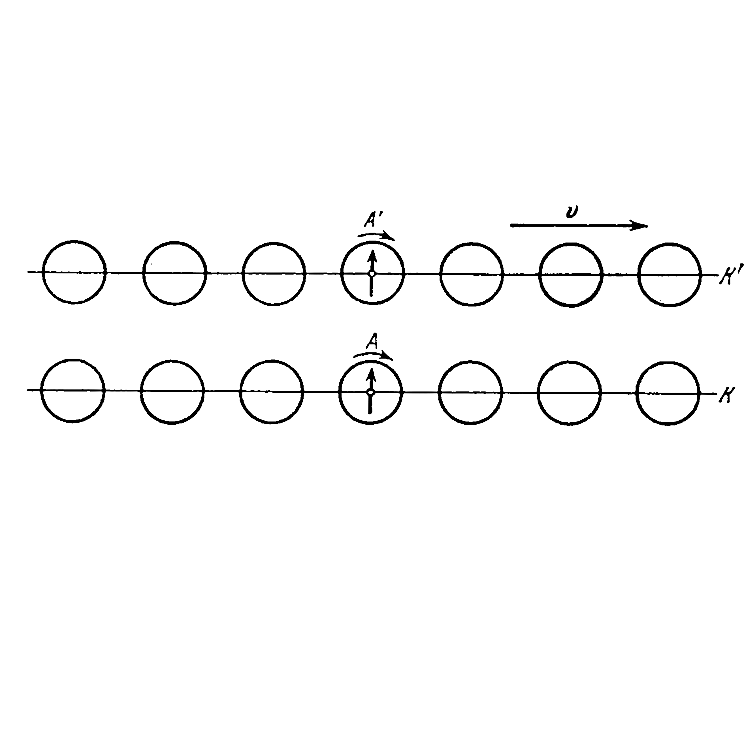
There are two groups of mutually synchronized clocks K and K′ moving relative to each other with a velocity v as shown in Figure. The moment when the clock A′ gets opposite the clock A is taken for the beginning of the time count. Draw the approximate position of hands of all the clocks at this moment "in terms of the K clocks", "in terms of the K′ clocks".
View SolutionA rod moves lengthwise with a constant velocity v relative to the inertial reference frame K. At what value of v will the length of the rod in this frame be η=0.5% less than its proper length?
View Solution
Knowledge Check
A conducting rod of length l is moving in a transverse magnetic field of strength B with veocity v. The resistance of the rod is R. The current in the rod is
ABlvRBBlvCzeroDB2v2l2R
A conducting rod of length l is moving in a transverse magnetic field of strength B with veocity v. The resistance of the rod is R. The current in the rod is
View SolutionTwo rods of the same proper length l0 move toward each other parallel to a common horizontal axis. In the reference frame fixed to one of the rods the time interval between the moments, when the right and left ends of the rods coincide, is equal to Δt. What is the velocity of one rod relative to the other?
View SolutionTwo rods having the same proper length l0 move lengthwise toward each other parallel to a common axis with the same velocity v relative to the laboratory frame of reference. What is the length of each rod in the reference frame fixed to the other rod?
View SolutionA rod moves along a ruler with a constant velocity. When the positions of both ends of the rod are marked simultaneously in the reference frame fixed to the rule, the difference of readings on the rule is equal to Δx1=4.0m. But when the positions of the rod's ends are marked simultaneously in the reference frame fixed to the rod, the difference of readings on the same ruler is equal to Δx2=9.0m. Find the proper length of the rod and its velocity relative to the ruler.
View SolutionA rod flies with constant velocity past a mark which is stationary in the reference frame K. In the frame K it takes Δt=20ns for the rod to fly past the mark. In the reference frame fixed to the rod the mark moves past the rod of Δt′=25ns. Find the proper length of rod.
View SolutionWith what velocity (relative to the reference frame K) did the clock move, if during the time interval t=5.0s, measured by the clock of the frame K, it becomes slow by Δt=0.10s?
View SolutionThe reference frame K′ moves in the positive direction of the x axis of the frame K with a relative velocity V′. Suppose that at the moment when the origins of coordinates O and O′ coincide, the clock readings at these points are equal to zero in both frames. Find the displacement velocity x of the point (in the frame K) at which the readings of the clocks of both reference frames will be permanently identical. Demonstrate that .x<V.
View Solution
