Find the efficiency of a cycle consisting of two isobaric and two isothermal lines if the pressure varies n−fold and the absolute temperature τ−fold within the cycle. The working substance is an ideal gas with the adiabatic exponent γ.
Here Q1''=CpT0(τ−1),Q'1''=τRT01nn and
Q2''=CpT0(τ−1),Q2'''=RT01nn
in addition to we have
Q1=Q1'+Q1'' and
Q2'=Q2''+Q2'''
So η=1−Q'2Q1=1−Cp(τ−1)+R1nnCp(τ−1)+τR1nn
=1−τ−1+(1−1γ)1nnτ−1+(1−1γ)τ1nn
=1−τ−1+(1−1γ)1nnτ−1+(1−1γ)τ1nn=(τ−1)1nnτ1nn+γ(τ−1)γ−1.
 .
.
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Liquids Capillary Effects25videos
THERMODYNAMICS AND MOLECULAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Phase Transformations35videos
THERMODYNAMICS AND MOLECULAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Kinetic Theory Of Gases51videos
THERMODYNAMICS AND MOLECULAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics49videos
PHYSICAL FUNDAMENTALS OF MECHANICS
Similar Questions
Find the efficiency of a cycle consisting of two isochoric and two isothermal lines if the volume varies v−fold and the absolute temperature τ−fold within the cycle. The working substance is an ideal gas with the adiabatic exponent γ.
View SolutionFind the efficiency of a cycle consisting of two isobaric and two adiabatic lines, if the pressure changes n times within the cycle. The working substance is an ideal gas whose adiabatic exponent is equal to γ.
View Solution
Knowledge Check
- Question 1 - Select One
The efficiency of the cycle shown below in the figure ( consisting of one isobar , one adiabatic and one isotherm ( is 50 % the ratio ,x, between the highest and lowest temperature attained in this cycle obeys ( the working substance is an ideal gas )
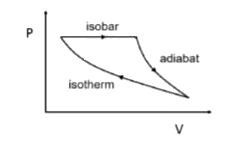 Ax=ex−1Bx2=ex−1Cx=ex2−1Dx2=ex2−1
Ax=ex−1Bx2=ex−1Cx=ex2−1Dx2=ex2−1 - Question 2 - Select One
An ideal gas goes through a cycle consisting of ischoric adiabatic and isothermal lines. The isothermal process is perform at minimum temperature. If the absolute temperature varies K times with tn the cycle then find out its effcincy.
 A1−lnKlB1+lnKlClnKlDllnK
A1−lnKlB1+lnKlClnKlDllnK
Calculate the efficiency of a cycle consisting of two isobaric and two adiabtic lines, if the pressure changes n=10 times within the cycle. The working substances is an ideal gas of adiabatic exponent γ=1.5.
View SolutionFind the efficiency of a cycle consisting of two isochoric and two adiabatic lines, if the volume of the ideal gas changes n=10 times within the cycle. The working substance is nitrogen.
View SolutionFind the efficiency of a cycle consisting of two isochoric and two adiabatic lines if the volume of the ideal gas changes n=10 times within the cycle. The working gas has γ=1.5.
View SolutionThe efficiency of the cycle shown below in the figure ( consisting of one isobar , one adiabatic and one isotherm ( is 50 % the ratio ,x, between the highest and lowest temperature attained in this cycle obeys ( the working substance is an ideal gas )
 View Solution
View SolutionAn ideal gas whose adiabatic exponent equals γ goes through a cycle consisting of two isochoric and two isobaric lines. Find the efficiency of such a cycle, if the absolute temperature of the gas rises n times both in a isochoric heating and in the isobaric expansion.
View SolutionCalculate the efficiency of a cycle consisting of isothermal, isobaric, and isochoric line, if in the isothermal process the volume of the ideal gas with the adiabatic exponent γ.
(a) increased n−fold ,
(b) decreases n−fold.View Solution

