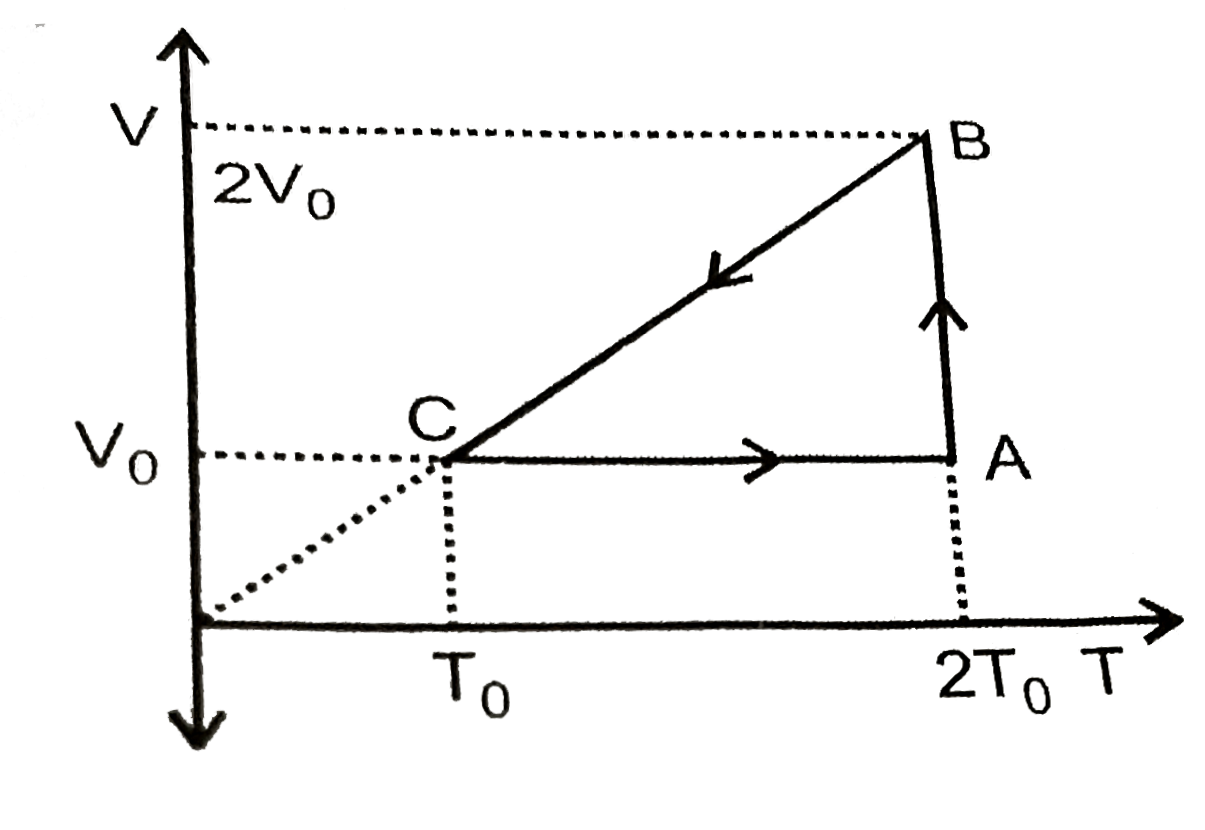
An ideal gas with the adiabatic exponent γ goes through a cycle (Fig. 2.3) within which the absolute temperature varies τ−fold. Find the efficiency of this cycle.
 .
.
Because of the linearity of the section
BC whose equation is
pp0=vVV0(=p=αV)
We have τv=v or v=√τ
Here Q''2=CVT0(√τ−1),
Q'''2=CpT0(1−1√τ)=CpT0√τ(√τ−1)
Thus Q'2=Q''2+Q'''2=RT0γ−1(√τ−1)(1+γ√τ)
Along BC, the specific heat C is given by
CdT=CVdT+pdV=CVdT+d(12αV2)=(CV+12)dT
Thus Q1=12RT0γ+1γ−1τ−1√τ
Finally η=1−Q'2Q1=1−2√τ+γ√τ+11γ+1=(γ−1)(√τ−1)(γ+1)(√τ+1).
 .
.
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Liquids Capillary Effects25videos
THERMODYNAMICS AND MOLECULAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Phase Transformations35videos
THERMODYNAMICS AND MOLECULAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Kinetic Theory Of Gases51videos
THERMODYNAMICS AND MOLECULAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics49videos
PHYSICAL FUNDAMENTALS OF MECHANICS
Similar Questions
One mole of an ideal gas with the adiabatic exponent γ goes through a polytropic process as a result of which the absolute temperature of the gas increases τ−fold. The polytropic constant equal n. Find the entropy increment of the gas in this process.
View SolutionAn ideal gas with the adiabatic exponent γ goes through a direct (clockwise) cycle conisting of adiabatic, isobaric, and isochoric lines. Find the efficiency of the cycle if in the adiabatic process the volume of the ideal gas.
(a) increases n-fold ,
(b) decreases n-fold.View Solution
Knowledge Check
- Question 1 - Select One
The efficiency of an ideal gas with adiabatic exponent 'γ' for the shown cyclic process would be
 A(2ln2−1)γ/(γ−1)B(1−2ln2)γ/(γ−1)C(2ln2+1)γ/(γ−1)D(2ln2−1)γ/(γ+1)
A(2ln2−1)γ/(γ−1)B(1−2ln2)γ/(γ−1)C(2ln2+1)γ/(γ−1)D(2ln2−1)γ/(γ+1) - Question 2 - Select One
The efficiency of an ideal gas with adiabatic exponent 'γ' for the shown cyclic process would be
 A(γ−1)(2 ln 2−1)1+(γ−1)2 ln 2B(γ−1)(1−2 ln 2)(γ−1)2 ln 2−1C(2 ln 2+1)(γ−1)(γ−1)2 ln 2+1D(2 ln 2−1)γ/(γ−1)
A(γ−1)(2 ln 2−1)1+(γ−1)2 ln 2B(γ−1)(1−2 ln 2)(γ−1)2 ln 2−1C(2 ln 2+1)(γ−1)(γ−1)2 ln 2+1D(2 ln 2−1)γ/(γ−1)
An ideal gas whose adiabatic exponent equals γ goes through a cycle consisting of two isochoric and two isobaric lines. Find the efficiency of such a cycle, if the absolute temperature of the gas rises n times both in a isochoric heating and in the isobaric expansion.
View SolutionA working substance goes through a cycle within which the absolute temperature varies n−fold, and the shape of the cycle is shown in
(a) Fig.a ,
(b) Fig. b, where T is the absolute temperature, and S the entropy. Find the efficiency of each cycle.
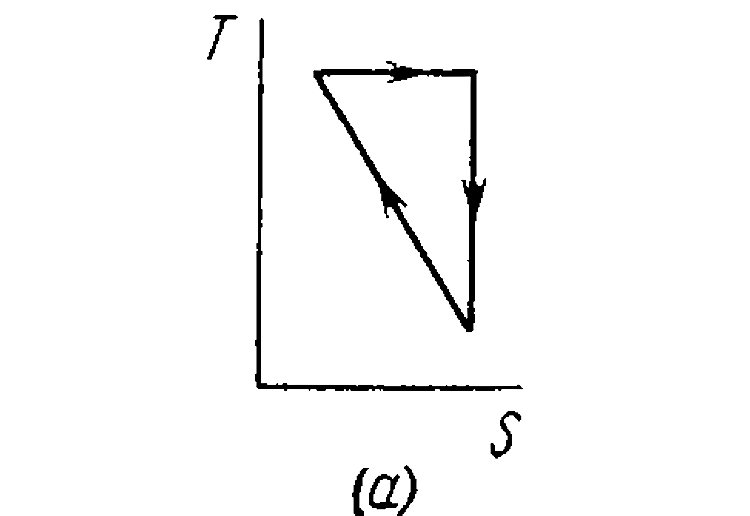
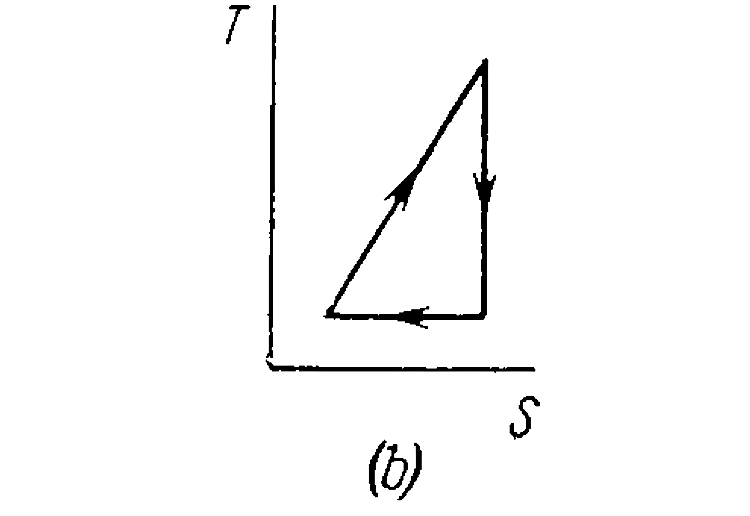 .View Solution
.View SolutionAn ideal monoatomic gas goes through a cyclic process. Ratio of maximum temperature and minimum temperature is 2. find efficiency of cycle.
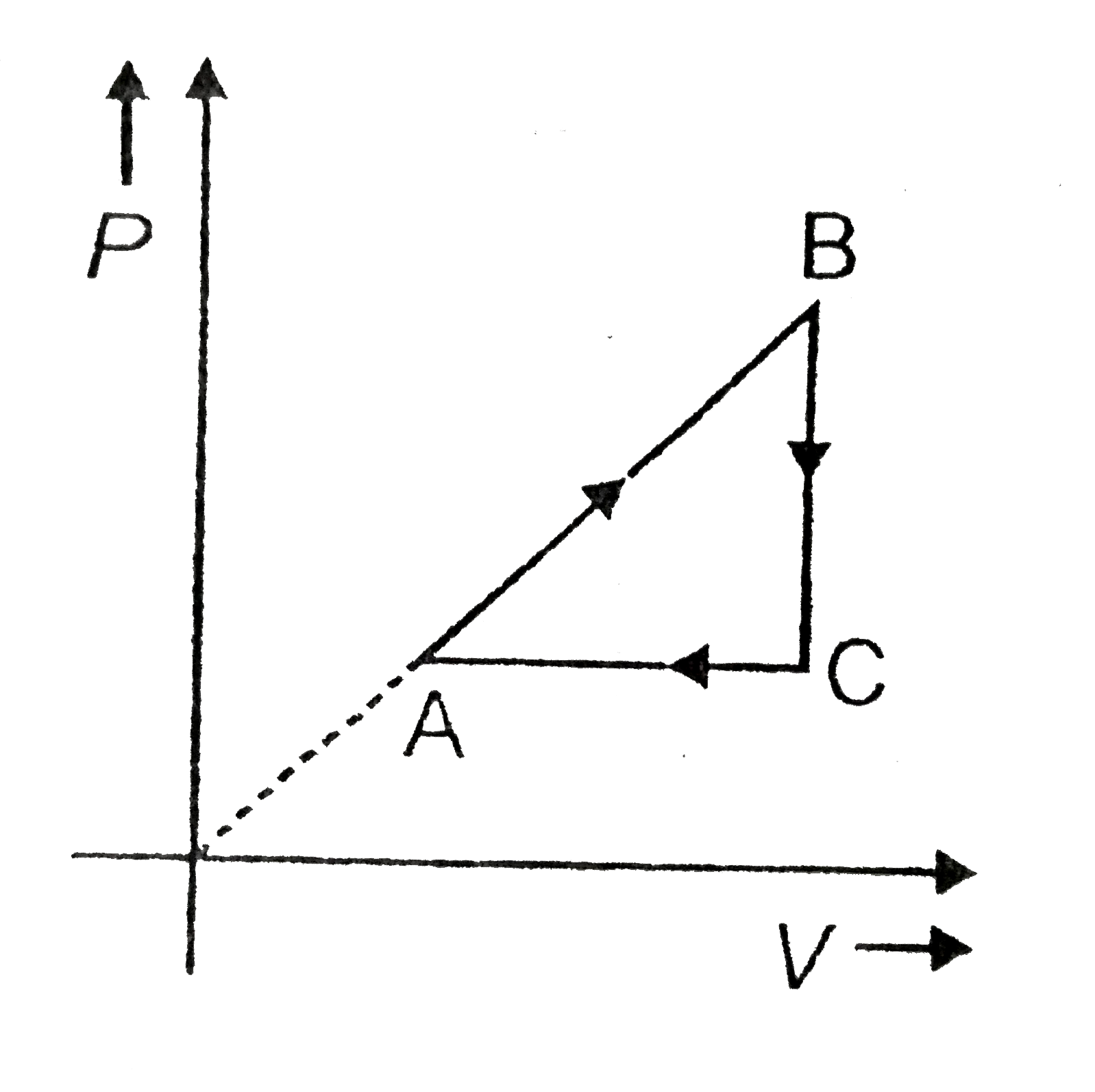 .View Solution
.View SolutionAn ideal gas with the adiabatic exponent γ goes through a process p=p0−αV, where p0 and α are positive constants, and V is the volume. At what volume will the gas entropy have the maximum value ?
View SolutionAn ideal gas goes through a cycle consisting of isothermal, polytropic, and adiabatic lines, with the isothermal process proceeding at the maximum temperature of the whole cycle. Find the efficiency of such a cycle if the absolute temperature varies n−fold within the cycle.
View SolutionAn ideal gas goes through a cycle consisting of
(a) isochoric, adiabatic, and isothermal lines ,
(b) isobaric, adiabatic, and isothermal lines,
with the isothermal process proceeding at the minimum temperature of the whole cycle. Find the efficiency of each cycle if the absolute temperature varies n−fold within the cycle.View Solution

