Calculate the efficiency of a cycle consisting of isothermal, isobaric, and isochoric line, if in the isothermal process the volume of the ideal gas with the adiabatic exponent $γ$ .
(a) increased $n - f o l d$ ,
(b) decreases $n - f o l d$ .

Video Solution

Text Solution

Verified by Experts

(a) $Q'_{2} = C_{p} T_{0} (1 - \frac{1}{n}), Q''_{1} = R T_{0} 1 n n, Q'_{1} = C_{V} T_{0} (1 - \frac{1}{n}), Q_{1} = Q'_{1} + Q''_{1}$
So $η = 1 - \frac{Q'_{2}}{Q_{1}} = 1 - \frac{C_{p} (1 - \frac{1}{n})}{C_{V} (1 - \frac{1}{n}) + R 1 n n}$
= $1 - \frac{γ}{1 + \frac{R}{C_{V}} \frac{n 1 n n}{n - 1}} = 1 - \frac{γ (n - 1)}{n - 1 + (γ - 1) n 1 n n}$
(b) $Q_{1} = C_{p} T_{0} (n - 1), Q''_{2} = C_{V} T_{0} (n - 1) Q'''_{2} = R T_{0} 1 n n, Q'_{2} = Q''_{2} + Q'''_{2}$
So $η = 1 - \frac{Q'_{2}}{Q_{1}} = 1 - \frac{n - 1 + (γ - 1) 1 n n}{γ (n - 1)}$ .

|

Updated on:21/07/2023

Class 12 PHYSICS THERMODYNAMICS AND MOLECULAR PHYSICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In an isothermal process the volume of an ideal gas is halved. One can say that
AInternal energy of the system decreases
BWork done by the gas is positive
CWork done by the gas is negative
DInternal energy of the system increases
Question 2 - Select One
The efficiency of an ideal gas with adiabatic exponent $' γ'$ for the shown cyclic process would be

A $\frac{(2 ln 2 - 1)}{γ / (γ - 1)}$
B $\frac{(1 - 2 ln 2)}{γ / (γ - 1)}$
C $\frac{(2 ln 2 + 1)}{γ / (γ - 1)}$
D $\frac{(2 ln 2 - 1)}{γ / (γ + 1)}$
Question 3 - Select One
The efficiency of an ideal gas with adiabatic exponent $' γ'$ for the shown cyclic process would be

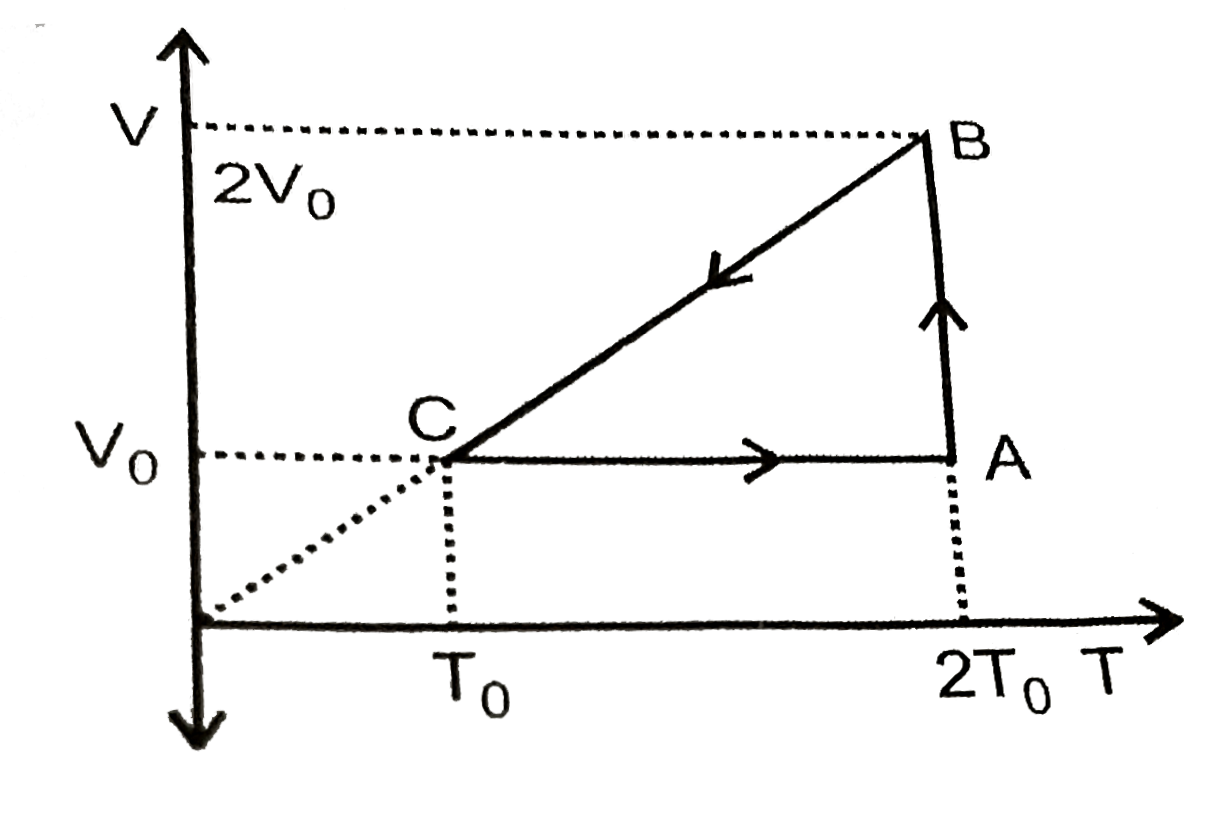A $\frac{(γ - 1) (2 ln 2 - 1)}{1 + (γ - 1) 2 ln 2}$
B $\frac{(γ - 1) (1 - 2 ln 2)}{(γ - 1) 2 ln 2 - 1}$
C $\frac{(2 ln 2 + 1) (γ - 1)}{(γ - 1) 2 ln 2 + 1}$
D $\frac{(2 ln 2 - 1)}{γ / (γ - 1)}$

IE IRODOV, LA SENA & SS KROTOV-THERMODYNAMICS AND MOLECULAR PHYSICS-The Second Law Of Thermodynamics - Entropy

Home
Ask Doubt
Profile