A thin straight rod of length 2a carrying a uniformly distributed charge q is located in vacumm. Find the magnitude of the electric field strength as a function of the distatance r from the rod's centre along the streaight line
(a) perpendicular to the rod and passing through its centre ,
(b) coinciding with the rod's direction (at the point lying outside the rod).
(a) It is clear from symmetry condiderations that vector →E must be directed as shwon in the figure. This shown the way of solving theis problem , we must find the component dE, of the field created by the element dl of the rod, having the charge dq and then intergation the result over all teh elements of the rod. In this case
dEr=dEcosα=14πε0λdlr20cosα,
whew λ=q2a is the linear charge density. Let us reduice this equaction this equaction of the from conventlent for intergation. Figure shows that dlcosα=r0α and r0=rcosα,
Consequently,
dEr=14πε0λr0dαr20=λ4πε0rcosαdα
This expression can be easily intergated :
E=λ4πε0r2∫α00cosαdα=λ4πε0r2sinα0
where α0 is the maximum value of the angle α,sinα0=a/√a2+r2
Thus, E=q/2a4πε0r2a√a2+r2=q4πε0r√a2+r2
Note that in this case also E=q4πε0r2 for r>>a as of the fiedld of a point charge.
(b) Let, us consider the element of length dl at a distanace l from the centre of the rod, as shown in fig.
Then field at P, due to this element.
dE=λdl4πε0(r−l)2,
If the element lies on teh side, shown in the diagram, and dE=λdl4πε0(r+l)2, if it lies on other side.
Hence E=∫dE=∫a0λ4πε0(r−l)2+∫a0λ4πε0(r+l)2
On intergating and putting λ=q2a, we get, E=q4πε01(r2−a2)
For r>>a,E=q4πε0r2


Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Conductors And Dielectrics In An Electric Field47videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field46videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
A thin straight rod of length l carrying a uniformly distributed charge q is located in vacuum. Find the magnitude of the electric force on a point charge 'Q' kept as shown in the figure.
 View Solution
View SolutionA point charge q is located at the centre fo a thin ring of radius R with uniformly distributed charge −q, find the magnitude of the electric field strength vectro at the point lying on the axis of the ring at a distance x from its centre, if x>>R.
View Solution
Knowledge Check
- Question 1 - Select One
Moment of inertia of a thin rod of mass 'M' and length 'L' about the axis perpendicular to the rod and passing through its centre is ............
AML24BML26CML212DML22 - Question 2 - Select One
A 10 cm long rod carries a charge of +150μC distributed uniformly along its length. Find the magnitude of the electric field at a point 10 cm from both the ends of the rod.
A15.6×107N/CB15.6×105N/CC1.56×107N/CD1.56×105N/C - Question 3 - Select One
If l1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and l2 is the moment of inertia (about central axis) of the ring formed by bending the rod, then the ratio of I1 to I2 is
Al:l=1:1Bl:l=π:3Cl:l=π:4Dl:l=3:5
A rod of length 20 cm carries a charge of +150 μC that is uniformly distributed along its length. Find the electric field intensity at a point, which is 20 cm away from both the ends of the rod.
View SolutionThe moment of inertia of a straight thin rod of mass M and length l about an axis perpendicular to its length and passing through its one end, is
View SolutionFigure 22-24 shows a plastic rod having a uniformly distributed charge. The charge per unit length of the rod is λ. Find the electric field due to the rod at a point P which is at a distance r from the rod.
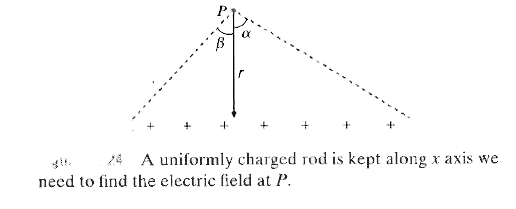 View Solution
View SolutionA rod of length L has a total charge Q distributed uniformly along its length. It is bent in the shape of a semicircle. Find the magnitude of the electric field at the centre of curvature of the semicircle.
View SolutionA rod of length l, has a uniform positive charge per unit length and a total charge Q. calculate the electric foeld at a point P located along the long axis of the rod and at a distance a from one end
 View Solution
View Solution

