An electric capacitor consists of this round parallel plates. each of radius R, separated by a distance l(l<<R) and uniformly charged with surface densities σ and −σ . Find the potential of the electirc field and the magnitude of tis strength vector at the axes of the capacitor as functions of a distanace x from the plates if x>>l. Investigate and obtained expressions at x>>R.
For x>0 we can use the result as given above and write
φ=σl2ε0(1−|x|(R2+x2)1/2)
for the solution that solution that vanishes at α . There is a discontiunity in potentail for |x|=0. The solution for negative x is obtained by σ→−σ. Thus
φ=σ/x2ε0(R+x2)1/2 + constant
Hence ignorning the jump
E=−∂φ∂x=σlR22ε0(R2+x2)3/2
for large |x|φ≈±p2πε0x2 and E≈p2πε0|x|3 (where p=πR2σl)
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Conductors And Dielectrics In An Electric Field47videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field46videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
Two this parallel threads carry a uniform charge with linear densities lamnda and −λ . The distance between the threads is equal to l. Find the potential of the electric field and the magnitude of its strength vector at the distance r>>l at the angle θ to the vector 1 (fig).
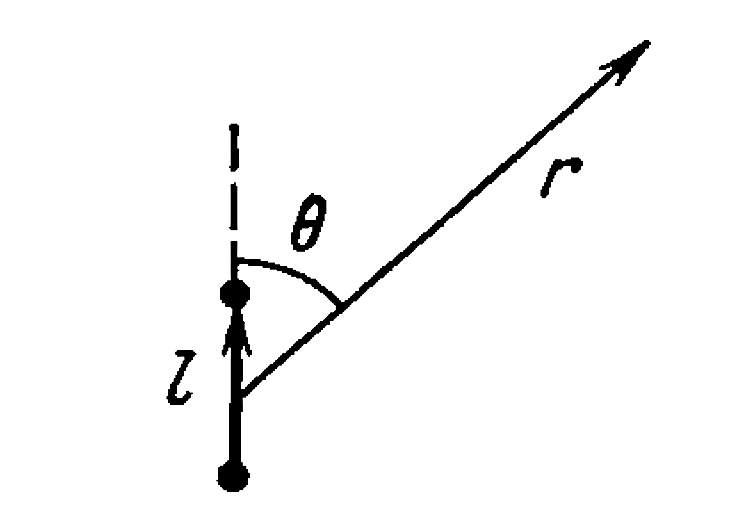 View Solution
View SolutionA very thin round plate of radius R carrying a uniform surface charge density σ is located in vacumm. Find the electric field potentail and strength along the plate's axis as a function of a distance l from its centre. Investigation the obtained expression of l→0 and l>>R.
View Solution
Knowledge Check
- Question 1 - Select One
Two large parallel conducting plates are placed close to each other ,the inner surface of the two plates have surface charge densities +σ and −σ .The outer surfaces are without charge.The electric field has a magnitude of
Aσε0 in the region between the platesBσε0 in the region outside the plates.C2σε0 in the region between the platesDzero in the region outside the plates. - Question 2 - Select One
Two large parallel conducting plates are placed close to each other ,the inner surface of the two plates have surface charge densities +σ and −σ .The outer surfaces are without charge.The electric field has a magnitude of
A(sigma)/(epsi_(0)) in the region between the platesB''σε0 in the region between the platesC0Dnone of these
Two coaxial rings, eacg of radius R, made of thin wire are separated by a small distabce l(l<<R) and carry the charges q and −q. Find the electric field potential and strength at the axis of the system as a function of the x coordinate (see figure). Investigate these functions at |x|>>R
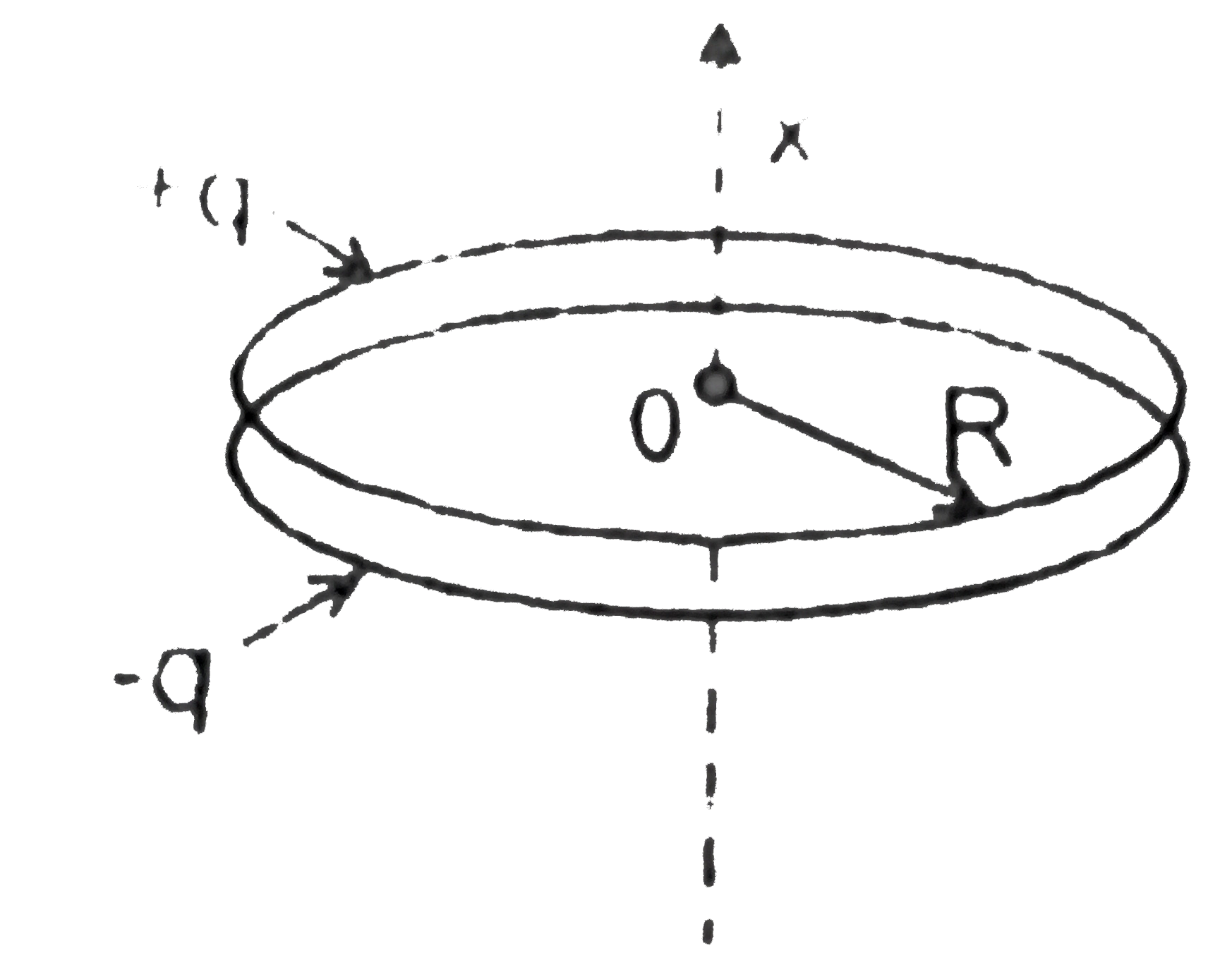 View Solution
View SolutionTwo coaxial rings, eacg of radius R, made of thin wire are separated by a small distabce l(l<<R) and carry the charges q and −q. Find the electric field potential and strength at the axis of the system as a function of the x coordinate (see figure). Investigate these functions at |x|>>R
 View Solution
View SolutionA ball of radius R is uniformly charged with the volume density ρ. Find the flux if the electric field strength vector across the balls section formed by the plane located at a distance r0<R from the centre of the ball.
View SolutionFind the potential φ at the edge of a thin disc of radius R carrying the uniformly distributed charge with surface density σ.
View SolutionA thin wire of radius ..r.. carries a charge q. Find the magnitude of the electric field strength on the axis of the ring as a function of distance L from the centre. Find the same for L>>r Find maximum field strength and the corresponding distance L.
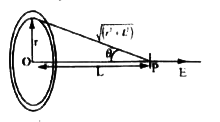 View Solution
View SolutionTwo thin infinite parallel plates have uniform charge densities +σ and −σ. The electric field in the space between them is
View Solution

