A long straight wire carrying a current I and a II- shaped conductor with siding connector are located in the same plane as shown in Fig. The connector of length l and resistance R sides to the right with a current induced in the loop as a function of separation r between the connector and the stragiht wire. The resistance of the II-shaped conductor and the self-induced of the loop are assumed to be negligible.

Field, due to the current carrying wire in the region, right to it, is directed into the plane of the paper and its magnitude is given by,
B=μ02πir where r is the perpendicular distance from the wire.
As B is same length of the rod thus motinal e.m.f
ξin=∣∣∣−∫21(→v×→B).d→l∣∣∣=vBl
and it is directed in the sense of (→v×→B)
So, current (induced) in teh loop,
iin=ξinR=12μ0IviπRr
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Motion Of Charged Particle In Magnetic Field
36 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Constant Magnetic Fiels - Magnetics
69 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
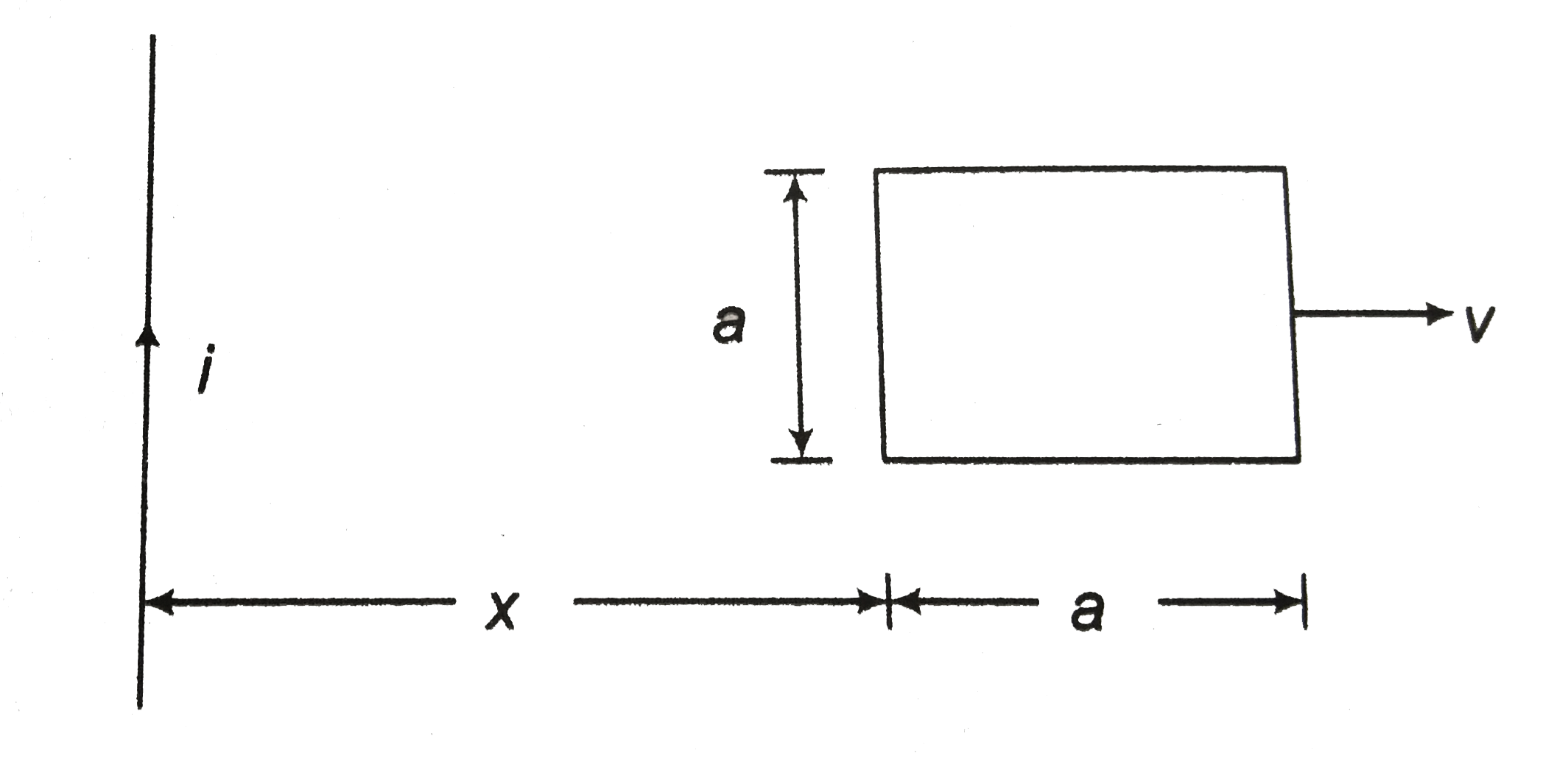
An infinitely long straight wire carrying current I , one side opened rectangular loop and a conductor C with a sliding connector are located in the same plane , as shown in the figure. The connector has length l and resistance R . It slides of the right with a velocity v. The resistance of the conductor and the self inductance of the loop are negligible . The induced current in the loop , as function of separation r between the conductor and the straight wire is :
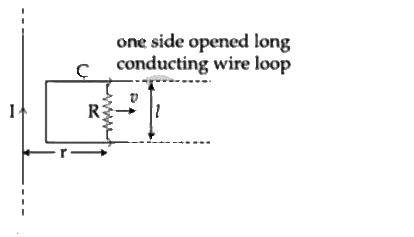
View SolutionA square frame with side a and a long straight wire carrying a current i are located in the same plane as m shown in figure. The fram translates to the right with a constant velocity v. Find the emf induced in the frame as a function of distance x.
View Solution
Knowledge Check
A straight conductor carrying current I and a loop closed by a sliding connector of resistance R lie in the same plane . The connector slides towards right with a uniform velocity v . The induced current generated in the loop in terms of distance r of the connector from the straight conductor will be __
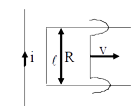 Aμ0ilv2πrBμ0il2πrCμ0ilv2πrRDNone of these
Aμ0ilv2πrBμ0il2πrCμ0ilv2πrRDNone of theseA long straight wire is carrying a current of 25 A. A square loop of side length 10 cm carrying a current of 15 A, is placed 2 cm from the wire as shown in figure. The force on the loop is
 A3.1×10−3N towards the wireB3.1×10−4N towards from the wireC9.4×10−4N towards the wireD9.4×10−4N away from the wire.
A3.1×10−3N towards the wireB3.1×10−4N towards from the wireC9.4×10−4N towards the wireD9.4×10−4N away from the wire.A long straight wire carrying current I and a square conducting wire loop of side l , at a distance 'a' from current wire as shown in the figure. Both the current wire and loop are in the plane of paper. Find the magnetic flux of current wire, passing through the loop.
Aμ02π.Illoge.a+IaBμ04π.Illoge.a+IaCμ02π.IlDμ04π.I
An infinitely long straight wire carrying a current I1 is partially surrounded by a loop as shown in Fig. The loop has a length L, radius R, and carries a current I2 The axis of the loop coincides with the wire. Calculate the force exerted on the loop.

View SolutionRelation between current in a conductor and time is shown in fig.

If the resistance of the conductor is R, then the total heat disspipated across resistance R is
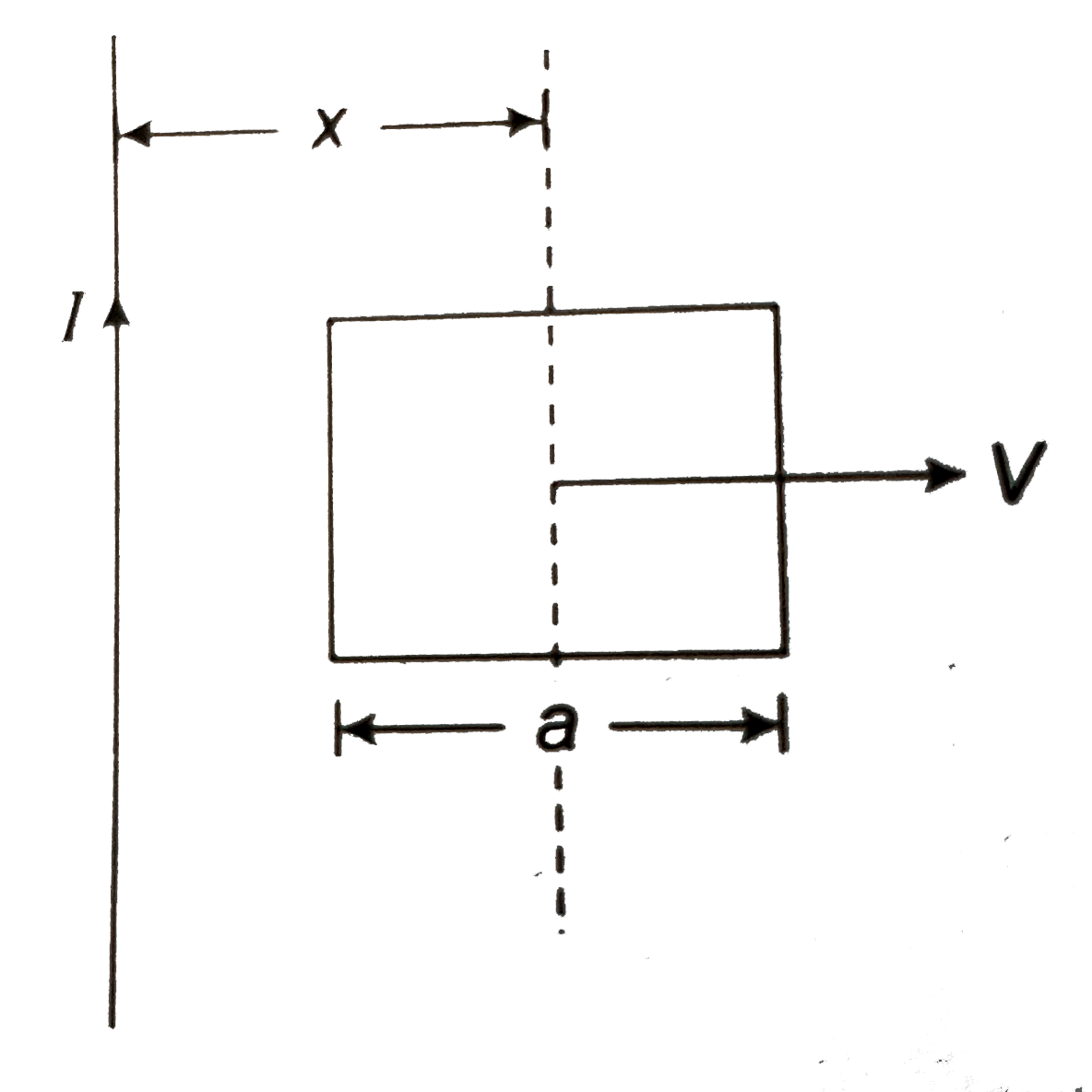
View SolutionA conducting square frame of side 'a' and a long straight wire carrying current I are located in the same plane as shown in the figure. The frame moves to the right with a constant velocity 'V'. The emf induced in the frame will be proportional to
View SolutionA loop and an infinite wire are placed side by side as shown in the figure. If the current I in the wire is increased then the induced current in the loop is
View SolutionA conductor AB of length L carrying a current I', is placed perpendicular to a long straight conductor XY carrying a current I as shown in Fig. The forces on AB has magnitude

View Solution
