A point charge q moves with a non-relativestic velocity v = const. Applying the theorem for the circulation of the vector H around the dotted circle shown in Fig, H at the point A as a function of a radius vector r and velocity v of the charge.

We use Maxwell's equations in the form,
∮→B.D→r=ε0μ0∂∂t∫→E.D→S,
when the condiuction current vanishes at the site.
We know that,
∫→Ed→S=q4πε0∫dΩ=q4πε02π(1−cosθ),
where, 2π(1−cosθ) is the solid angle, formed by the disc like surfac, at the charge.
Thus, ∮→B.d→r=2πaB=12μ0qsinθ.θ
On the other hand x=acotθ
differening and using dxdt=−v
v=acosec2θθ
Thus, B=μ0qvrsinθ4πr3
This can be written as, →B=μ0q(→v×→r)4πr3
and →H=q4π→v×→rr3 (The sense has to be checked independently.)

Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Motion Of Charged Particle In Magnetic Field
36 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Constant Magnetic Fiels - Magnetics
69 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
A point charge q moves with a non-relatives velocity v = const. Find the displacement current density .d at a point location at a distance r from the charges on a straight line
(a) coinciding with the charge path,
(b) perpendicualr to the path and passing through the charge.
View SolutionA non-relativistic point charge q moves with a constant velocity v. Using the field transformation formula. Find the magnetic induction B produced by this charge at the point whose position relative to the charge is determind by the radius vector r.
View Solution
Knowledge Check
On rotating a point charge g around a charge Q in a circle of radius r, the work done is
Aq.2πrBq.2πOrCzeroDQ2ε0rA particle of charge q is projected from point P with velocity v as shown. Choose the correct statement from the following.
 AMagnetic field at P is μ0i4πr[2+√2]⊙BThe magnetic field at P is μ0i/2πr.CThe particle initially accelerated towards wire A.DThe particle initially accelerated towards wire B.
AMagnetic field at P is μ0i4πr[2+√2]⊙BThe magnetic field at P is μ0i/2πr.CThe particle initially accelerated towards wire A.DThe particle initially accelerated towards wire B.A point positive charge of Q' units is moved round another point positive charge of Q units in circular path. If the radius of the circle r is the work done on the charge Q' in making one complete revolution i-
AQ4π∈0rBQQ'4π∈0rCQ'4π∈0rD0
A point charge q moves unifromly and rectilnearly with a relativistic with a relativistic velocity of light (β=v/c). Find the electric field strength E produced by the charge at the point whose radius vector relatives to the charge is equal to r and forms an angle θ with its velocity vector.
View SolutionA point charge +q is moved with a constant velocity v toward a solid conducting sphere carrying a charge Q. Find the (a) potential of the sphere, (b) charge induced as the function of r, (c ) charge flowing if we close the key K, and (d) current is the part (c ).
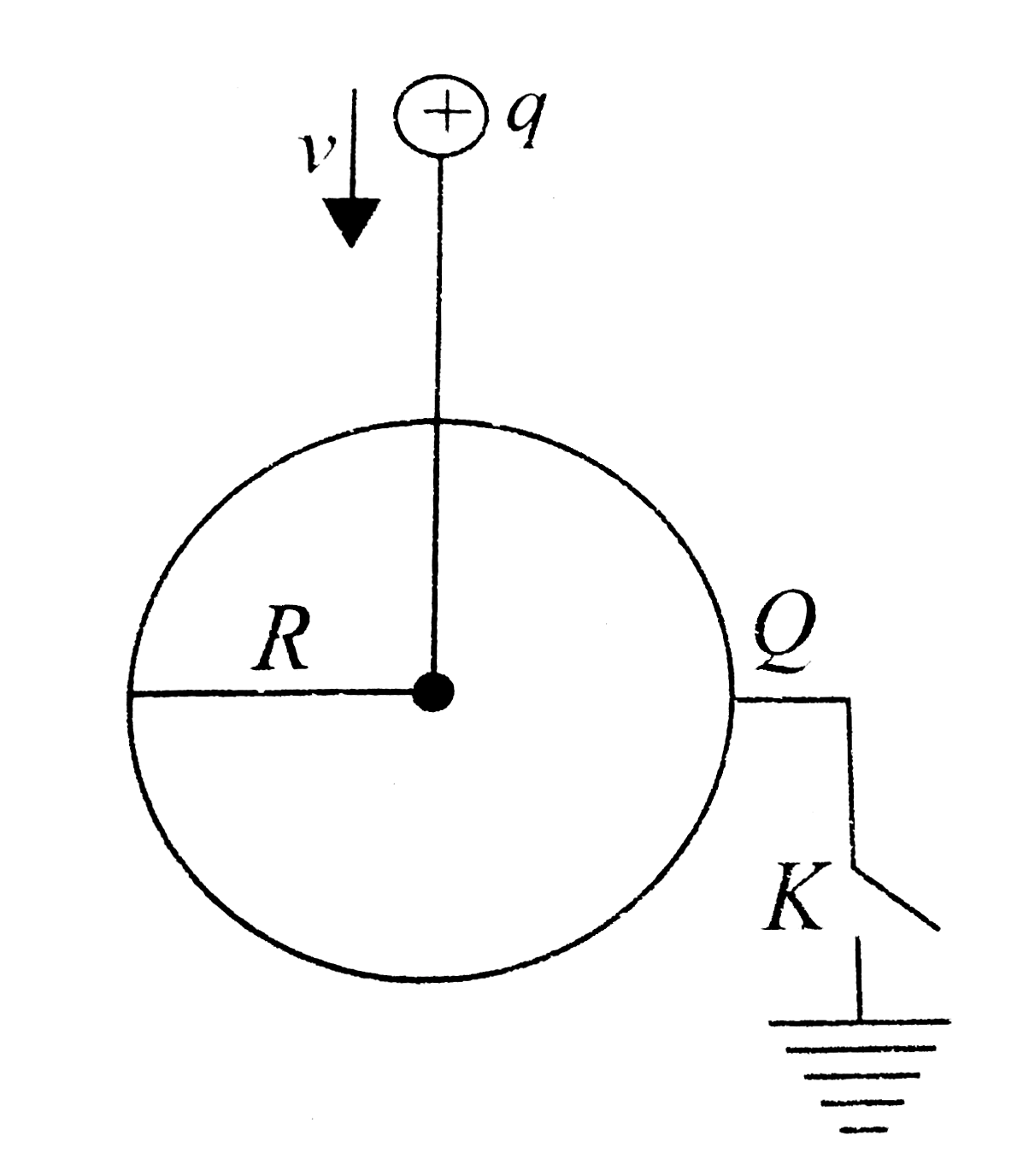
View SolutionA particle is moving with a constant speed v in a circle. What is the magnitude of average velocity after half rotation?
View SolutionA point charge q moving with a velocity →v at a given time in a magnetic field →B experiences a force given as F=q[→v.→B]
View SolutionWhen an electron of charge , e and mass , m moves with velocity v around the nuclear charge 'Ze' describing the circular orbit, the potential energy of the electron is
View Solution