A long solid aluminum cylinder of radius a=5.0cm rotates about its axis in unidrom magnetic field with induction B=10mT. The angluar velocity of rotation equlas ω=45rad/s with ω↑↑B Neglecting the magnetic field of appearing chagres, find their spcae and surfaface densities.
Choose →ω↑⏐⏐↑⏐⏐→B along the z-axis and choose →r, as the cylindrical polar radius of a reference point (perpendicular distance from the axis). This point has the velocity.
→v=→ω×→r,
and experiences a (→v×→B) force, which must be counterbalanced by an electric field,
→E=−(→ω×→r)×→B=−(→ω.→B)→r.
There must appear a space charge density,
ρ=ε0÷→E=−3ε0→ω→B=−8pC/m3
Since the cylinder, as a whole is electrically neutral the surface of the cylinder must acquire a positive charge of surface density,
σ=+2ε0(→ω.→B)πa22πa=ε0a→ω.→B=±2pC/m2
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Motion Of Charged Particle In Magnetic Field
36 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Constant Magnetic Fiels - Magnetics
69 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
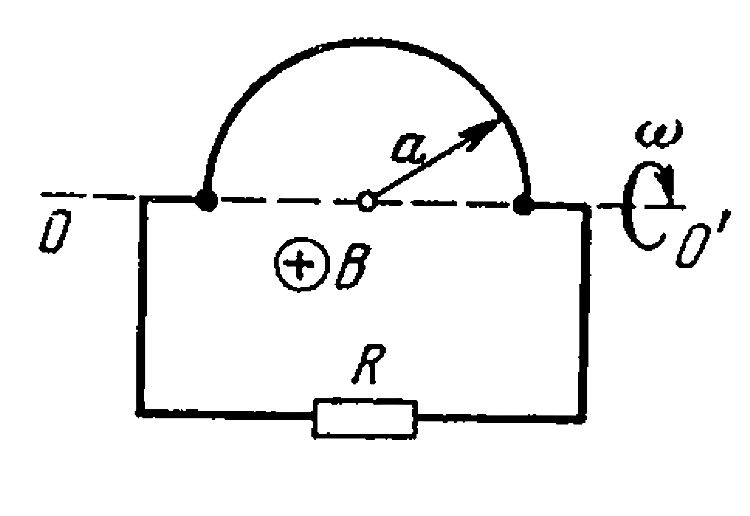
A wire shaped as a semi-circle of radius a rotates about sn sxis OO' with an angular velocity ω in a unifrom magnetic field of induction B' (Fig). The rotation axis is perpendicular to the field direction. The total resistance of the circuit is equal to R. NEglecting the magnetic field of the induced current, find the meand amount of thermal power being generated in the loop fueing a rotation period.
View SolutionIn a certain region of the inertial reference frame there is magnetic field with induction B rotating with angluar velocity ω. Find ∇×E in this region as a function of vectors ω and B
View SolutionA thin uniformly charged ring of radius a=10cm rotates about its axsi with an angluaar velocity ω=100rad/s. Find the ratio of volume energy densities of magnetic and electric fields on the axis of the ring at a point removed from its centre by a distance l=a
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA circular wire of radius r rotates about its own axis with angular speed w in a magnetic field B perpendicular to its plane, then the induced e.m.f. is
View SolutionA thin wire AC shaped as a semi-circle of diaameter d=20cm rotates with a constant angular velocity ω=100 rad/s in a unifrom magnetic field of induction B=5.0mT, with ω↑↑B. The rotation axis passes through the end A of the wire and is perpendicular to the diameter AC. Find the value of a line intergal ∫Edr along the wire from point A to C. Generalize the botained result.
View SolutionA cylinder of radius R full of liquid of density p is rotated about its axis at w rad/s. The increase in pressure at the centre of the cylinder will be
View SolutionA cylinder of radius R full of liquid of density p is rotated about its axis at w rad/s. The increase in pressure at the centre of the cylinder will be
View Solution
