A body of mass m is suspended from a spring fixed to the ceiling of an elevator car. The stiffness of the spring is x. At the moment t=0 the car starts going up with an accelerationw. Neglecting the mass of the spring , find the law of motion y(t0 of the body relative to the elevator car if y(0)−0 and y(0)=0. Consider the following two cases :
(a) w=const,
(b) w=αt, where αis a constant.
As the elevator car is a translating non− inertial frame, therefore the body m will experience an inertial force mw directed downward in addition to the real forces in the elevator's frame. From the Newton's second law in projection from
Fy=mwy for the body in the frame of elevator car :
−k(mgk+y)+mg+mw=m..y ....(A)
(Because the initial elongation in the spring is mg/k)
so, m..y=−ky+mw=−k(y−mwk)
or, d2dt2(y−mwk)=−km(y−mwk)...(1)
Eqn. (1) shows that the motion of the body m is S.H.M. and its solutino becomes
y−mwk=asin(√kmt+α)....(2)
Differentiating Eqn (2) w.r.t. time
.y=a√kmcos(√kmt+α)....(3)
Using the initial considiton y(0)−0 in Eqn (2), we get :
asinα=−mwk
and using the other initial condition .y(0)=0 in Eqn (3)
we get a√kmcosα=0
Thus α=−α/2and a=mwk
Hence using these values in Eqn (2), we get
y=mwk(1−cos√kmt)
(b) Proceed up to Eqn (1) . The solution of this differential Eqn be of the form :
y−mwk=asin(s√kmt+δ)
or,y−αtk/m=asin(√kmt+δ)
or, y=αtω20=asin(ω0t+δ) (where ω0=√km)...(4)
From the initial condition that at t=0,y(0), so 0=asinδ or δ=0
Thus Eqn, (4) takes the from :y−αtω20=asinω0t...(5)
Differentiating Eqn. (5), we get :.y−αω20=aω0cosωt....(6)
But from the other initial condition .y0(0)=0 at t=0
So, from Eqn. (6) −αω20=aω0 or a=−α/ω30
Putting the value of a in Eqn. (5), we get the sought y(t).e.i,
y−αtωt0=−αω30sinω0t or y=αω30(ω0t−sinω0t)
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations56videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves39videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise2videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics49videos
PHYSICAL FUNDAMENTALS OF MECHANICS
Similar Questions
A pulley fixed to the ceiling of an elevator car carries a thread whose ends are attached to the loads of masses 3m and m . The car starts gong up with acceleration g/s. Assuming the masses of the pulley and the thread, as well as friction, to be negligible, find the force exerted by the pulley on the ceiling of car.
 View Solution
View SolutionA body of mass m was suspended by a non-stretched spring, and then set fre without push. The stiffness of the spring is x. Neglecting the mass of the spring , find :
(a) the law of motion y(t), whee y is displacement of the body from the equilibrium position,
(b) the maximum and minimum tensions of the spring in the process of motion.View Solution
Knowledge Check
- Question 1 - Select One
A body of mass m is suspended from a massless spring of natural length l. It stretches the spring through a vertical distance y. The potential energy of the stretched spring is
Amg(l+y)B12mg(l+y)C12mgyDMgy - Question 2 - Select One
A mass is suspended from a spring have spring constant k is displaced veritcally and relased it oscillates with period T the weight of the mass suspended is (g= gravitatioanal acceleration)
AkTg4π2BkT2g4π2CkTg2π2DkT2g2π2 - Question 3 - Select One
A mass is suspended from a spring have spring constant k is displaced veritcally and relased it oscillates with period T the weight of the mass suspended is (g= gravitatioanal acceleration)
AkTg4π2BkT2g4π2CkTg2π2DkT2g2π2
A spring mass system is hanging from the ceiling of an elevator in equilbrium Elongation of spring is l. The elevator suddenly starts accelerating downwards with acceleration g/3 find.
(a) the frequency and
(b) the amplitude of the resulting SHM
 View Solution
View SolutionA pulley fixed to the ceiling of an elevator car carries a thread whose ends are attached to the masses m1andm2. The car starts going up with an acceleration a0. Assuming the masses of the pulley and the thread as well as the friction to be negligible, find:
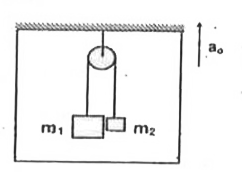
(a) the acceleration of the load m1 relative to the elevator shaft and relative to the car
(b) the force exerted by the pulley on the ceiling of the car. Given m1>m2.View SolutionA pulley fixed to the ceiling of an elevator car carries a thread whose ends are attached to the loads of masses m1 and m2. The car starts going up with an acceleration wo. Assuming the masses of the pulley and the thread, as well as the friction, to be negligible find:
(a) the acceleration of the load m1 relative to the elevator shaft and relative to the car,
(b) the force exerted by the pulley on the ceiling of the car.View SolutionSuppose the ceiling in the previous problem is that the elevator which is going up with an acceleration of 2.0ms2. Find the elongations.
View SolutionA spring mass system is hanging from the ceiling of an elevator in equilibrium. The elevator suddenly starts accelerating upwards with acceleration a, consider all the options in the reference frame of elevator.
 View Solution
View Solution

