Solve the foregoing problem for the case of the pan having a mass M. Find the oscillation amplitude in this case.
Text Solution
Unlike the previous (4.40) problem the kinetic energy of body m decreases due to the perfelcty inelastic collision with the pan. Obviously the body m comes to strike the pan with velocity v0=√2gh. If v be the common velocity of the '' body m+ pena system due to the collision thrn from the conservation of linear momentum
mv0=(M+m)v
or v=mv0(M+m)=m√2gh(M+m)...(1)
At the moment the body m strikes the pan, the spring is compressed due to weight of the pan by the amount Mg/k. If l be the further compression fo the spring due to the velocity acquired by the pan − body m system, then from the conservatiion of mechanical energy of the said system in the field generated by the joint action of boty the gravity and spring forces
12(M+m)v2+(M+m)gl=12k(Mgk+l)2−12k(Mgk)2
or, 12(M+m)m22gh(M+m)+(M+m)gl=12k(Mgk)2+12kl2−Mgl−12k(Mgk)2 (Using 1)
or, 12kl2−mgl−m2gh(m+M)=0
Thusl=mg±√m2g2+2kghm2M+mk
As minus sign is not acceptable
l=mgk+1k√m2g2+2km2gh(M+m)
If the oscillating " pan + body m system were at rest it correspong to their equilibrium position i.e. the spring were compressed by (M+m)gk therefore the amplitude of oscillation
a=l−mgk=mgk√1+2hkmg
The mechanical energy of oscillation which is only conserved with the restoring forces becomes E=Uextreme=12ka2( Because spring force is the only restoring force not the weight of the body )
Alternately E=Tmean=12(M+m)a2ω2
thus E=12(M+m)a2(kM+m)=12ka2
|
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
Knowledge Check
In the case of sustained force oscillations the amplitude of oscillations
Adecreases linearlyBdecreases sinusodiallyCdereases exponentiallyDalways remains constantIf maximum velocities of both the SHMs is same then find the ratio of amplitudes of the two cases
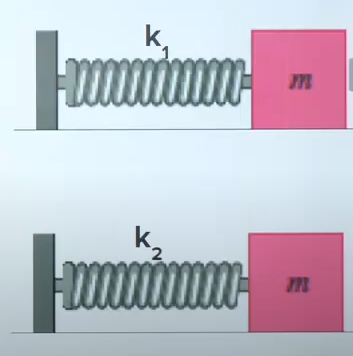 A√k2k1B√k1k2Ck2k1Dk1k2
A√k2k1B√k1k2Ck2k1Dk1k2
Solve the foregoing problem for the case of two concentric spheres of radii R1 and R2 and temperatures T1 and T2.
View SolutionSolve the same problem for the case of a weight suspended from a thin rod of negligible mass.
View SolutionSolve the previous problem for the cases of an isochoric, an isobaric and an isothermic process.
View SolutionSolve the foregoing problem if λ1=λ2=λ
View SolutionMaking use of the result obtained in the foregoing problem, find the conditions defining the angular position of maxima of the first, the second, and the third order.
View SolutionSolve the foregoing problem, assuming that the discs are located in an ultra-rarefied gas of molar mass M, at temperature T and under pressure p.
View Solution

