A pendulum is constructed as a light thin $-$ walled sphere of radius $R$ filled up with water and suspended at the point $O$ from a light rigid rod (figure). The distance between the point $O$ and the centre of the sphere is equal to $l$ . How many times will the small oscillations of such a pendulum change after the water freezes ? The visxosity of water and the change of its volume on freezes? The viscosity of water and the change of its volume on freezing are to be necglected.

Video Solution

Text Solution

Verified by Experts

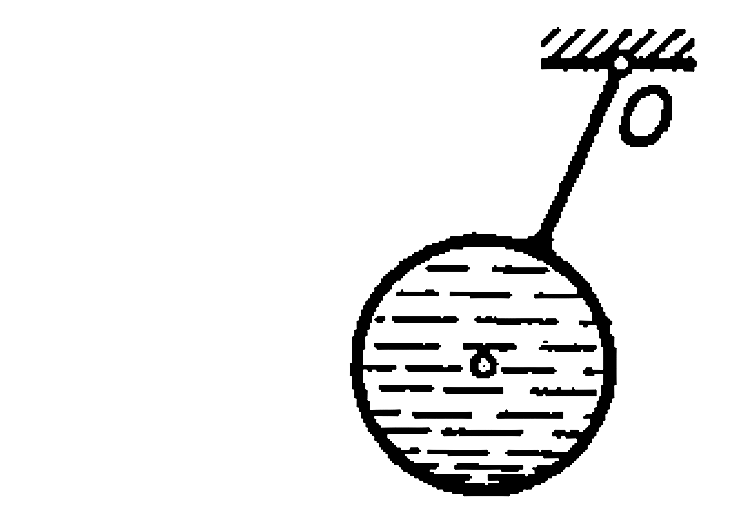
If water has frozen, the system consisting of the light rod and the frozen water in the hollow sphere constitute a compound (physical ) pendulum to a very good approximation because we can take the whole system to be rigid. For such systems the time period is given by
$T_{1} = 2 π \sqrt{\frac{l}{g}} \sqrt{1 + \frac{k^{2}}{l^{2}}}$ where $k^{2} = \frac{2}{5} R^{2}$ is the radius of gyration of the sphere. The situation is different when water is unfrozen. When dissipative froces (viscosity) are neglected, we are dealing with idal fluids. Such fluids instantaneously respond to $($ unbalanced $)$ internal stresses. Suppose the sphere with liquid water actually executes small rigid oscillation. Then the portion of the fluid above the centre of the sphere will have a greater acceleration than the portion below the centre because the linear acceleratino of any element is in this case, equal to angular acceleration of the element multiplied by the distance of the element from the centre of suspension $($ Recall that we are considering small oscillations $)$ . Then, as is obvious in a frame moving with the centre of mass, there will appear an unbalanced couple $($ not negated by any pseudoforces $)$ which will cause the fluid to move rotationally so as to destroy in acceleration. Thus for this case of ideal fluids the pendulum must in such a way that the elements of the fluid all undergo the same acceleration. This implies that we have a simple $($ mathematical $)$ pendulum with the time period $:$
$T_{0} = 2 π \sqrt{\frac{l}{m}}$
Thus $T_{1} = T_{0} \sqrt{1 + \frac{2}{5} {(\frac{R}{l})}^{2}}$
$($ One expects that a liquid with very small viscosity will have a time period close $T_{0}$ while one with high viscosity will have a time period closer to $T_{1})$ .

Updated on:21/07/2023