Two balls with massesm1=1.0kg and m2=2.0kg are slipped on a thin smooth horizontal rod ( figure). The balls are interconnected by a light spring of stiffness x=24N/m. The left- hand ball is imparted the initial velocity v1=12cm/s. Find :
(a) the oscillation frequency of the system in the process of motion,
(b) the energy and the amplitude of oscillations

Suppose the balls 1 & 2 are displaced by x1,x2 from their initial position. Then the energy is :E=12m1x21+m2.x2+m2.x2+12k(x1−x2)2=12m1v21
Also total mometum is :m1.x1+m2.x2=m1v1
DefineX=m1x1+m1x2m1+m2,x=x1−x2
Then x1=X+m2m1+m2x,x2=X−m1m1+m2x
E=12(m1+m2)X2+12m1m2m1+m2.x2+12kx2
Hence .X=m1v1m1+m2
So 12m1m2m1+m2.x2+12kx2+12m1v1−12m21v21m1+m2=12m1m2m1+m2v21
(a) From the above equation
We see ω=√kμ=√3×242=6s−1, whenμ=m1m2m1+m2=23kg.
(b) The energy of oscillation is
12m1m2m2+m2v21=1223×(−0.12)2=48×10−4=4.8mJ
We have x=asin(ωt+α)
Initially x=0 at t=0 so α=0
Then x=asinωt. Alstox=v1 at t=0
So, ωa=v1 and hence a=v1ω=126=2cm.
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations56videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves39videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise2videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics49videos
PHYSICAL FUNDAMENTALS OF MECHANICS
Similar Questions
Two bodies with masses m1 = 1kg and m2= 2kg are connected by a spring of force constant k=24Nm−1. The left ball is imparted an initial velocity v0=12 cm/s. Find (a) the frequency of the oscillations (b) the energy and the amplitude of the osciallations.
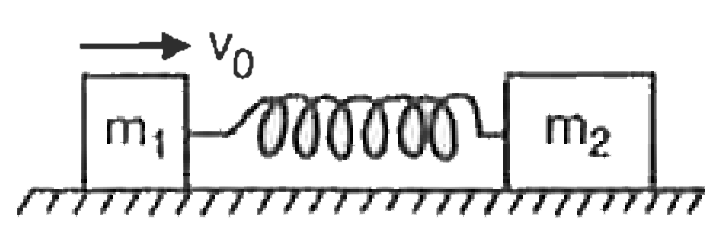 View Solution
View SolutionThe blockA(2kg) and B(3kg) rest up on a smooth horizontal surface are connected by a spring of stiffness 120N/m. Identially the spring is underformd. A is imparted a velocity of 2m/s along the line of the spring away from B. Find the displacement of A at t seconds later.
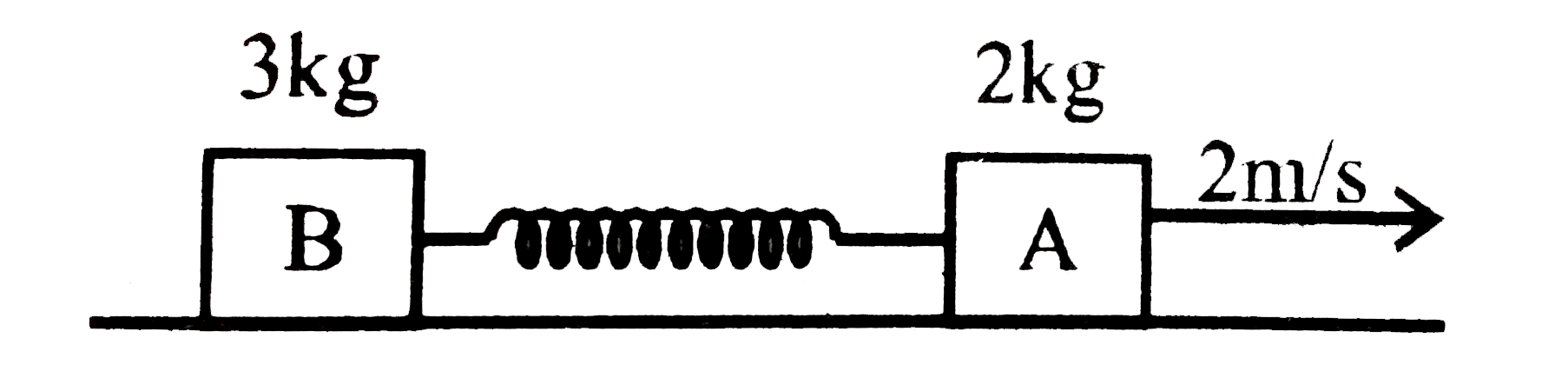 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two balls with masses m1=1kg and m2=2kg are slipped on a thin smooth horizontal rod as shown. The balls are interconnected by a light spring of stiffess K=24N/m. The left hand ball (m1) is imparted the initial velocity 12cm/s towards second ball. the amplitude of oscillations made by the arrangement is............
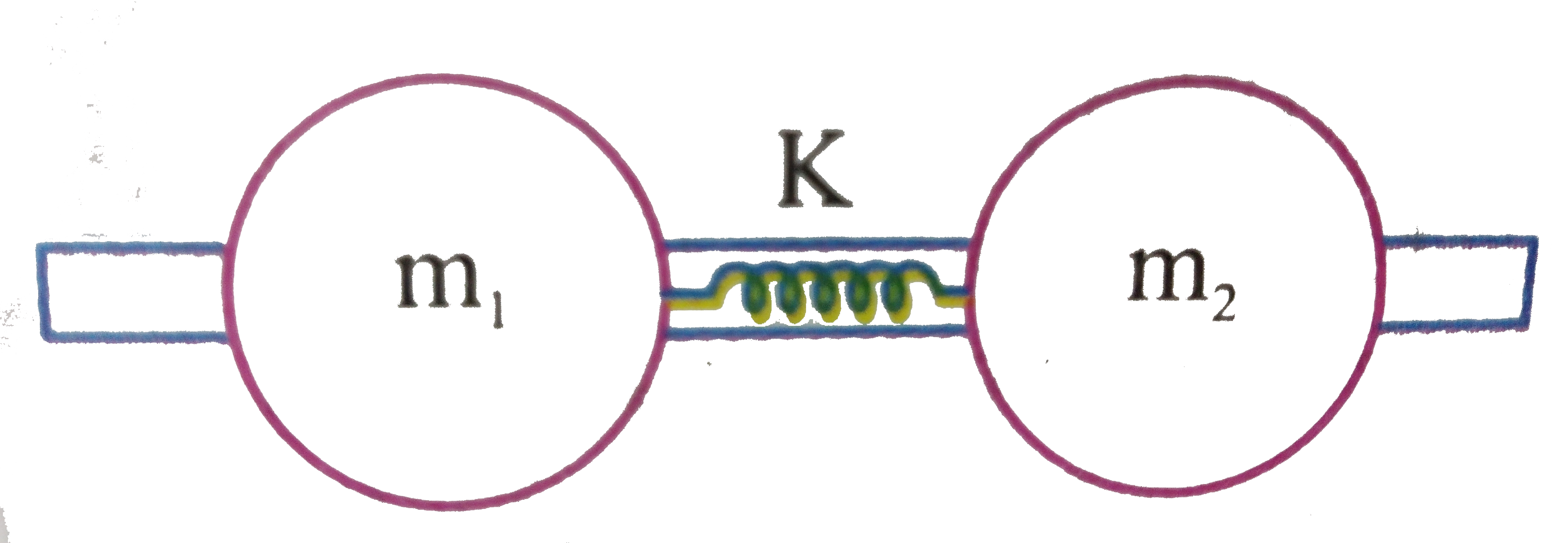 A3cmB2cmC1cmD4cm
A3cmB2cmC1cmD4cm - Question 2 - Select One
Two identical particles each of mass 0.5kg are interconnected by a light springs of stiffness 100N/m, time period of small oscillation is ….
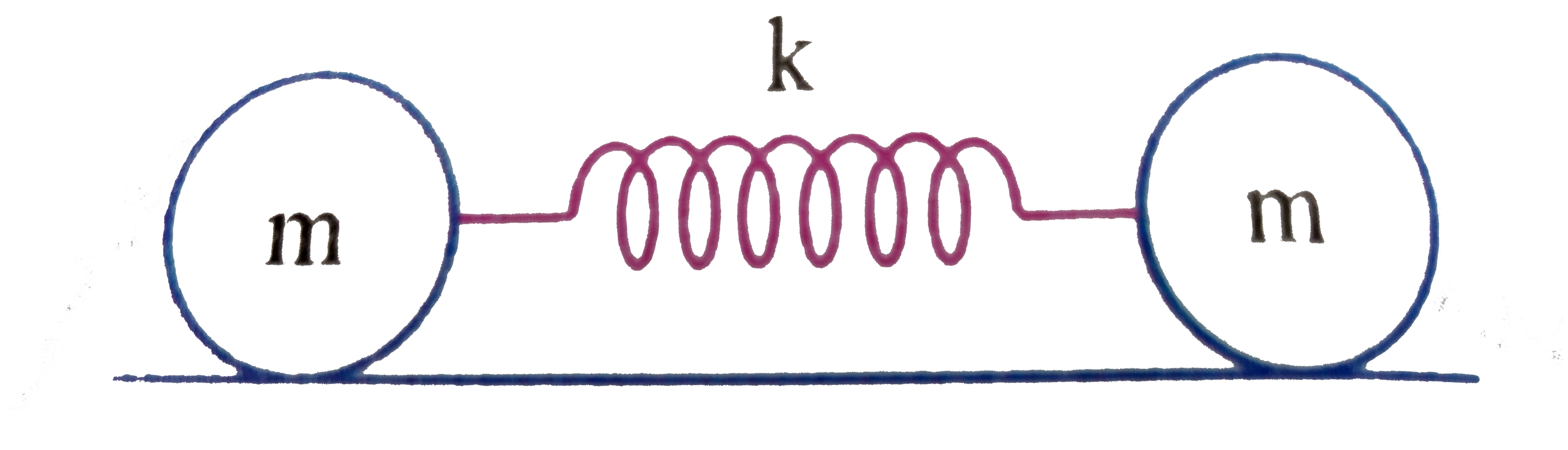 Aπ5√2Bπ10√2sCπ5sDπ10s
Aπ5√2Bπ10√2sCπ5sDπ10s - Question 3 - Select One
A ball of mass m=1kg strikes a smooth horizontal floor as shown in figure. The impulse exerted on the floor is
 A(a) 6.25NsB(b) 1.76NsC(c) 7.8NsD(d) 2.2Ns
A(a) 6.25NsB(b) 1.76NsC(c) 7.8NsD(d) 2.2Ns
Two blocks A (2 kg) and B (3 kg) rest on a smooth horizontal surface, connected by a spring of stiffness k = 120 N/m. Initially, the spring is relaxed. At t = 0, A is imparted a velocity u = 2 m/s towards right. Find displacement of block A as a function of time.
 View Solution
View SolutionTwo balls with masses m1=3kg and m2=5kg have identical velocity V=5m/s in the direction shwon in figure. They collide at origin. Find the distance of position of C.M. from the origin 2sec after the collision.
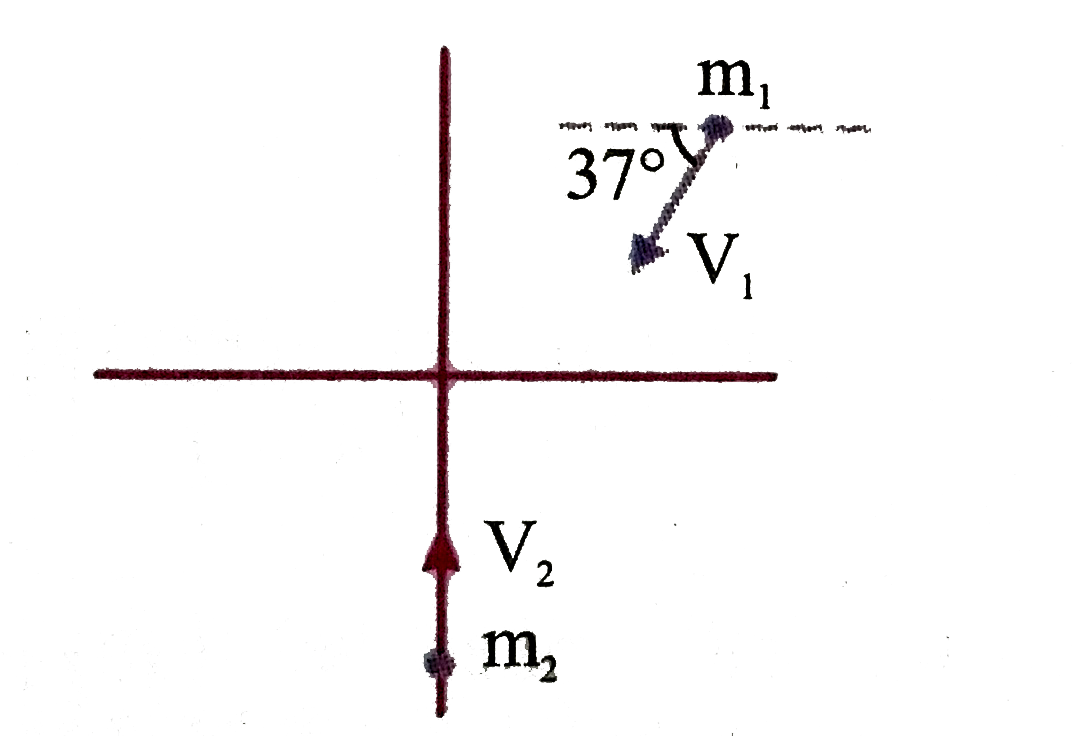 View Solution
View SolutionTwo cubes of mass m1 and m2 are interconnected by a weightless spring of stiffness k and placed on a smooth horizontal table. Then the cubes are drawn closer to each other and released. Find the frequency of oscillation.
 View Solution
View SolutionTwo blocks A(3kg) and B(2kg) resting on a smooth horizontal surface is connected by a spring of stiffness 480N/m. Initially the spring is underformed and a velocity of 2m/s is imparted to A along the line of the spring away from B. The maximum extension in meters of the spring during subsequent motion is :-
View SolutionTwo blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of osciallation is
View Solution

