In a cylinder filled up with ideal gas end gas and closed from both ends there is a piston of mass $m$ and cross $-$ sectional area $S$ (figure).In equilibrium the piston divides the cylinder into two equal parts, each with volime $V_{0}$ . The gas ppressure is $p_{0}$ . The piston was slightly displaced from the equlibrium position and released.Find the oscillation frequency, assuming the prosecces in the gas to be adiabatic and the friction negligible.

Video Solution

Text Solution

Verified by Experts

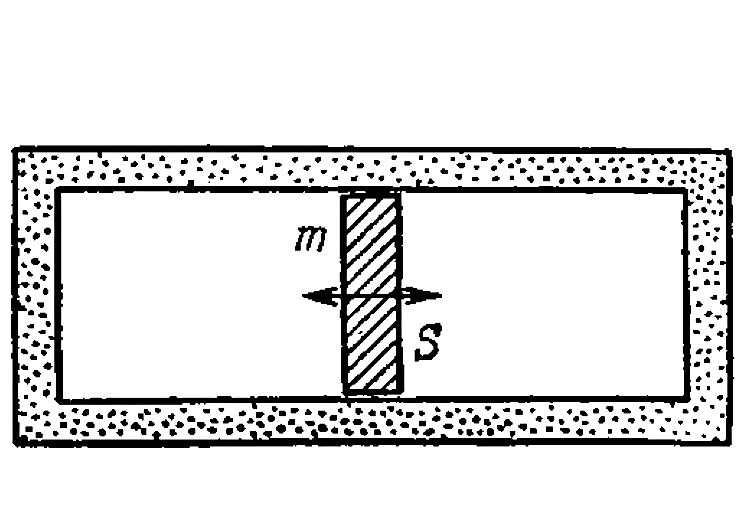
Let, us displace the pistone through small distance $x$ , towards right , then from $F_{x} = m w_{x}$
or, $(p_{1} - p_{2}) S = - m .. x ... (1)$
But, the process is adiabatic, so from $P V^{γ} =$ const.
$p_{2} = \frac{p_{0} V_{0}^{γ}}{{(V_{0} - S x)}_{0}^{γ}}$ and $p_{1} = \frac{p_{0} V_{0}^{γ}}{{(V_{0} + S x)}_{0}^{γ}}$
as the new volumes of the left and the right parts are now $(V_{0} + S x)$ and $(V_{0} - S x)$ respectively.
So, the Eqn (1) becomes.
$\frac{p_{0} V_{0}^{γ} S}{m} {\frac{1}{{(V_{0} - S x)}_{0}^{γ}} - \frac{1}{{(V_{0} + S_{x})}_{0}^{γ}}} = - .. x$
or, $\frac{p_{0} V_{0}^{γ} S}{m} {(\frac{{(V_{0} + S x)}_{0}^{γ} - {(V_{0} - S x)}_{0}^{γ}}{{(V_{0}^{2} - S^{2} x^{2})}^{γ}}} = - .. x$
$\frac{p_{0} V_{0}^{γ} S}{m} ⎧ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎩ \frac{(1 + \frac{γ S x}{V_{0}}) - (1 - \frac{γ S x}{V_{0}})}{V_{0}^{γ} (- \frac{γ S^{2} x^{2}}{V_{0}^{2}})} ⎫ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎭ = - .. x$
Neglecting the term $\frac{γ S^{2} x^{2}}{V_{0}^{2}}$ in the denominator, as it is very small, we get,
$.. x = \frac{2 p_{0} S^{2} γ x}{m V_{0}}$
which is the equation for $S . H . M$ . and hence the oscillating frequency.
$ω_{0} = S \sqrt{\frac{2 p_{0} γ}{m V_{0}}}$

Updated on:21/07/2023

Class 12 PHYSICS OSCILLATIONS AND WAVES

Topper's Solved these Questions

Knowledge Check

A closed and isolated cylinder contains ideal gas. An adiabatic separator of mass m, cross sectional area $A$ divides the cylinder into two equal parts each with volume $V_{0}$ and pressure $P_{0}$ in equilibrium Assume the sepatator to move without friction.
If the piston is slightly displaced by x, the net force acting on the piston is
A $\frac{P_{0} γ A^{2} x}{V_{0}}$
B $\frac{2 P_{0} γ A^{2} x}{V_{0}}$
C $\frac{3 P_{0} γ A^{2} x}{V_{0}}$
D $\frac{P_{0} γ A^{2} x}{(γ - 1) V_{0}}$
An ideal gas enclosed in a cylindrical container supports a freely moving piston of mass $M$ . The piston and the cylinder have equal cross-sectional area $A$ . When the piston is in equilibrium, the volum of the gas is $V_{0}$ and its pressur is $P_{0}$ . The pistong is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
A $\frac{1}{2 π} \frac{γ A P_{0}}{V_{0} M}$
B $\frac{1}{2 π} \frac{V_{0} M P_{0}}{γ A^{2}}$
C $\frac{1}{2 π} \sqrt{\frac{γ A^{2} P_{0}}{M V_{0}}}$
D $\frac{1}{2 π} \sqrt{\frac{M V_{0}}{γ^{2} P_{0}}}$
An ideal gas enclosed in a vertical cylindrical container supports a freely moving pistion of mass M. The pistion and the cylinder have equal cross sectional area A. When the pistion is in equilibrium, the volume of the gas is $V_{0}$ and its pressure is $P_{0}$ . The pistion is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the pistion executes a simple harmonic motion with frequency
A $\frac{1}{2 π} \frac{A γ P_{0}}{V_{0} M}$
B $\frac{1}{2 π} \frac{V_{0} M P_{0}}{A^{2} γ}$
C $\frac{1}{2 π} \sqrt{\frac{A^{2} γ P_{0}}{M V_{0}}}$
D $\frac{1}{2 π} \sqrt{\frac{M V_{0}}{A γ P_{0}}}$

IE IRODOV, LA SENA & SS KROTOV-OSCILLATIONS AND WAVES-Electromagnetic Waves, Radiation

Home
Ask Doubt
Profile

Topper's Solved these Questions

Similar Questions

Knowledge Check

IE IRODOV, LA SENA & SS KROTOV-OSCILLATIONS AND WAVES-Electromagnetic Waves, Radiation