A particle of mass m can perform undamped harmonic oscillations due to an electric force with coefficient k. When the particle was in equilibrium, a permanent force F was applid to to its for τ seconds. Find the oscillation amplitude that the particle acquired after the action of the force ceased. Draw the approximate plot x(t) of oscillations. Investigate possible cases.
We have to look for solutions of the equation
m..x+kx=F,0<t1<x
m..x+kx=0,t>τ
subject to x(0)=.x(0)=0 where F is constant.
The solution of this equation will be sought in the form
x=Fk+Acos(ω0t+α),0≤t≤τ
x=Bcos(ω0(t−τ)+β),t>τ
A and τ will be determined from the baoundary condition at t=0.
0=Fk+Acosα
0=−ω0Asinα
Thus, α=0 and A=−Fk and x=Fk(1−cosω0t)0≤t<τ.
B and β will be determiing by the continuity of x and .x at t=τ. Thus Fk(1−cosω0τ)=Bcosβ and cancel(omega_(0))(F)/(k) sin omega_(0) tau=- cancel( omega_(0))B sin beta
Thus B2=(Fk)2(2−2cosω0τ)
or B=2Fk∣∣∣sin(ω0τ2)∣∣∣

Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
A ball of mass m can perform undamped harmonic oscillations about the point x=0 with natural frquency, ω0. At the moment t=0, when the ball was in equilibrium, a force Fx=F0cosωt coinciding with the x axis was applied to it. Find the law of forced oscillation x(t) for that ball.
View SolutionAt the moment t=0 a particle of mass m starts moving due to a force F=F0sinωt, where F0 and ω are constants. Find the distance covered by the particle as a function of t. Draw the approximate plot of this function.
View Solution
Knowledge Check
A particle of mass m excuting SHM make f oscillation per second. The difference of its kinetic energy when at the centre, and when at distance x from the centre is
Aπ2f2x2mB2π2f2x2mC12π2f2x2mDf2x2mEquation of motion for a particle performing damped harmonic oscillation is given as x=e−1tcos(10πt+ϕ). The time when amplitude will half of the initial is :
A27B4C1D7
A particle of rest mass m0 starts moving at a moment t=0 due to a constant force F. Find the time dependence of the particle's velocity and of the distance covered.
View SolutionA particle of mass m is free to move along x axis under the influence of a conservative force. The potential energy of the particle is given by U=−axxe−bx [a and b are positive constants]
Find the frequency of small oscillations of the particle about its equilibrium position
View SolutionTwo mass m1 and m2 are suspended from a massless spring of force constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. Find the angular frequency and amplitude of oscillations.
View SolutionA particle of mass = 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is nπ5 second. Find value of n.
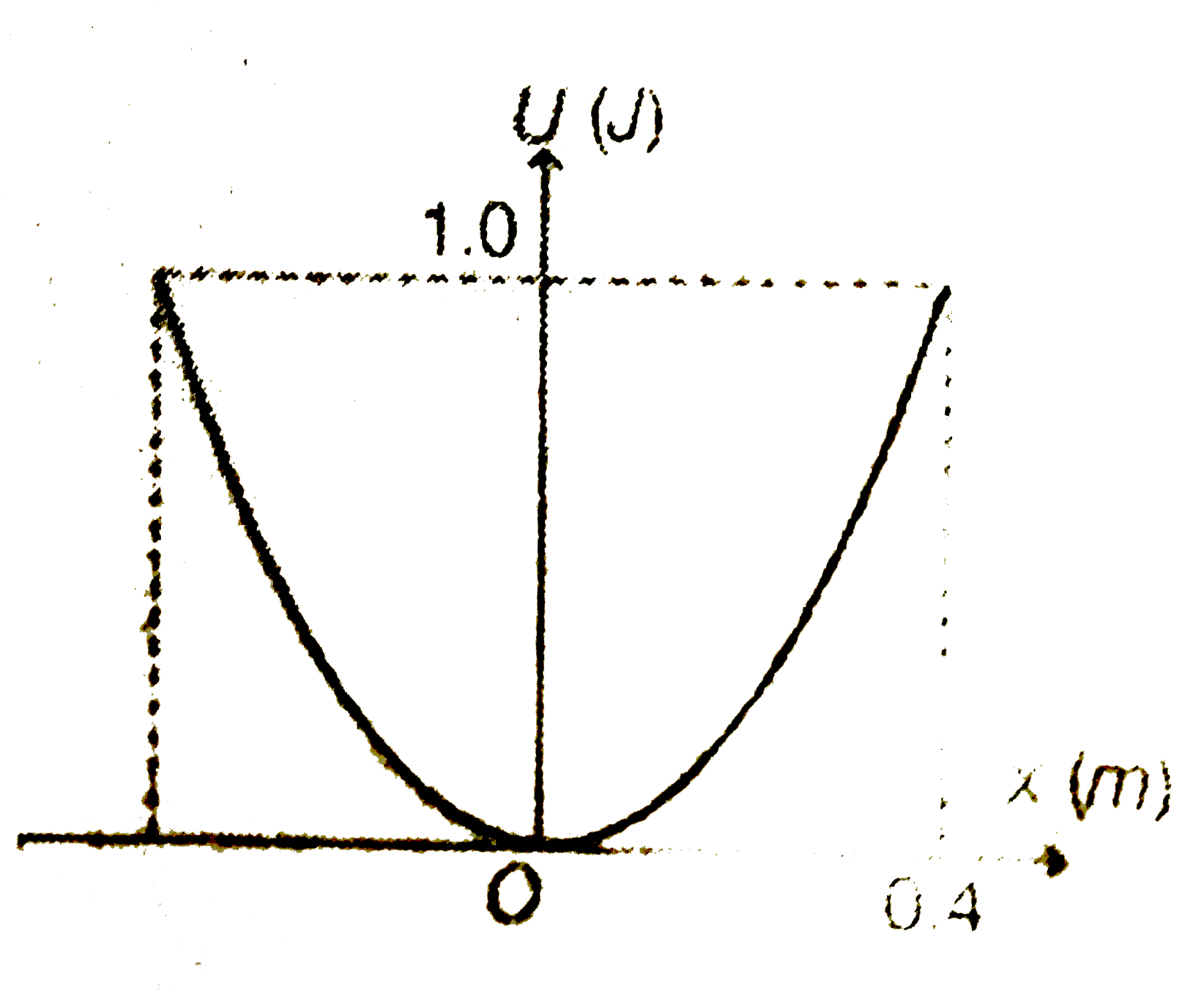
View SolutionA particle of mass 0.50 kg executes a simple harmonic motion under a force F = – (50 N/m)x. If it crosses the centre of oscillation with a speed of 10 m/s, find the amplitude of the motion.
View SolutionA particle of mass 0.50 kg executes a simple harmonic motion under a force F=−(50Nm−1)x. If it crosses the centre of oscillation with a speed of 10ms−1, find the amplitude of the motion.
View Solution
