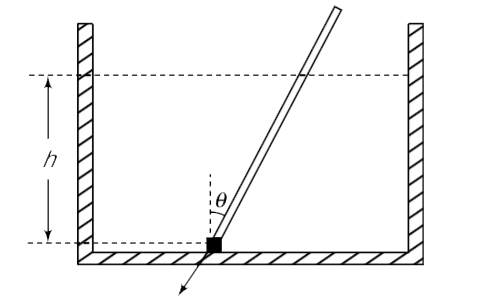
A man standing on the bottom. The depth o fthe swimming pool looks at a stone lying on the bootom. The depth of the swimming pool is equal to h. At what distance from the surafce of water is the image of the stone formed if the line of vision makes an angle θwith the normal to the surface?
From the Fig.
sindα=MPOM=MNcosαhsec(α+dα)
As dα is very small, so
dα=MNcosαHsecα=MNcos2αh (1)
Similarly
dθ=MNcos2θh' (2)
From Eqn (1) and (2)
dαdθ=h'cos2αhcos2θ or, h'=hcos2θcos2αdαdθ
From the law of refraction
nsinα=sinθ (A)
sinα=sinθn, so, cosα=√n2−sin2θn2 (B)
Differentiating Eqn (A)
ncosαdα=cosθdθ or, dαdθ=cosθncosθ (4)
Using (4) in (3), we get
h'=hcos3θncos3α (5)
Hence h'=hcos3θn(n2−sin2θn2)3/2=n2hcos3θ(n2−sin2θ)3/2 [Using Eqn (B)]

Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Interference Of Light33videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Diffraction Of Light60videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems92videos
MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
Similar Questions
A stone S is on the bottom of a swimming pool. The depth of the lying pool is d and index of refraction of water is μ. What is the depth of the swimming pool visible to a normal eye ? Cheak the results with d=6ft and μ=1.5.
View SolutionA rectangular tank contains water to a height h. A metal rod is hinged to the bottom of the tank so that it can rotate freely in the vertical plane. The length of the rod is L and it remains at rest with a part of it lying above the water surface. In this position the rod makes an angle θ with the vertical. Assume thaty=cosθ and find fractional change in value of y when temperature of the system increases by a small value ΔT.Coefficient of linear expansion of material of rod and the tank areα1 and α2 respectively. Coefficient of volume expansion of water is λ. What is necessary condition for θ to increase?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A man standing in a swimming pool looks at a stone lying at the bottom. The depth of the swimming pool is h. At what distance from the surface of water is the image of the stone formed -
Ah/μBhμCμ/hDh - Question 2 - Select One
A man stnading in a swimming pool looks at a stone lying at the bottom. The depth of the swimming pool is h. At what distance from the surface of water is the image of the stone formed? (Line of vision is normal, Refractive index of water is n)
Ah/nBn/hChDhn - Question 3 - Select One
What is the real depth of a swimming pool when its bottom appears to be raised by 1 m ? Given refractive index of water is 4/3.
A2mB16mC4mD8m
Water stands at a depth H in a tank whose side walls are vertical. A hole is made on one of the walls at a depth h below the water surface. Find at what distance from the foot of the wall does the emerging stream of water strike the floor and for what value of h this range is maximum ? What is the maximum possible range ?
View SolutionIn a swimming pool, a person is viewing outside objects by keeping an eye at a depth h inside water. If the critical angle for water is ‘ θc’, then the value of the diameter of the circle of view for outside objects will be
View SolutionA fish is swimming in a pool whose bottom surface is silver polished. Find where an observer in the air will observe the image of the fish if the depth of the pool is H and the fish is at depth h below the water surface?
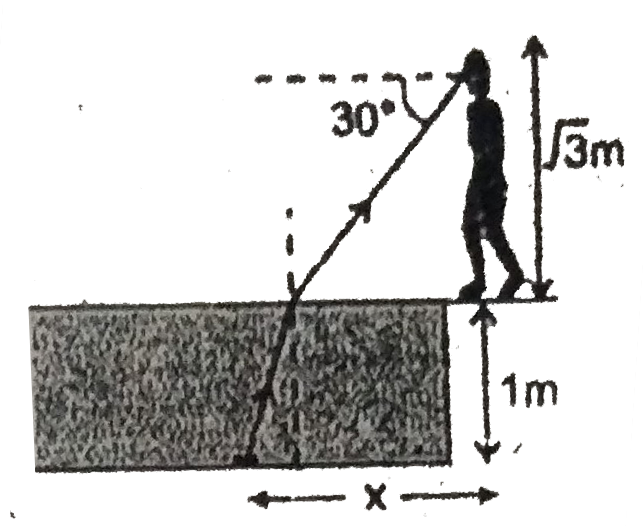
View SolutionA man is standing at the edge of a 1m deep swimming pool, completely filled with a liquid of refractive index √32. The eyes of the man are √3m above the ground. A coin located at the bottom of the pool appears to be an angle of depression of 30∘ with reference to the eyes of man. Then horizontal distance (represented by x in the figure) of the coin from the eye of the man is ...........mm.
 View Solution
View SolutionA bird is flying over a swimming pool at a height of 2m from the water surface. If the bottom is perfectly plane reflecting surface and depth of swimming pool is 1m, then the distance of final image of bird from the bird itself is μw=4/3
View Solution

