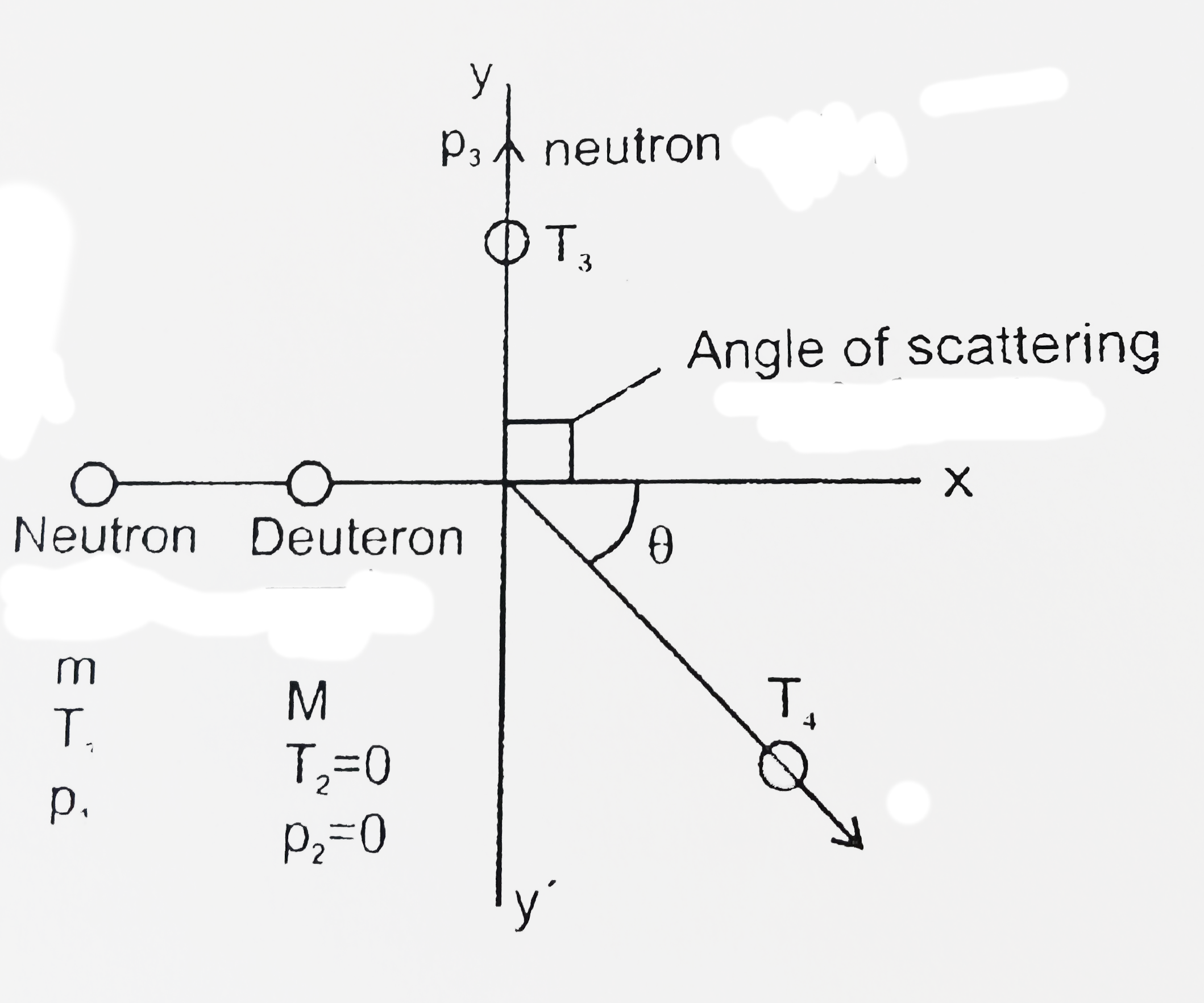
A neutron collides elastically with an initially stationary deuteron. Find the fraction of the kinetic energy lost by the neutron (a) in a head-on collision , (b) in scattering at right angles.

Text Solution

Verified by Experts

The correct Answer is:(a) $η = 4 m M / {(m + M)}^{2} = 0.89$
(b) $η = 2 m / (m + M) = 2 / 3$
Here $m$ and $M$ are the masses of a neutron and deutron.

According conservation principal of momentum,
${\to p}_{1} + {\to p}_{2} = {\to p}_{3} + {\to p}_{4}$
or $p_{1} = p_{3} + p_{4}$ .....(4)
According conservation principle of kinetic energy
$T_{1} + T_{2} = T_{3} + T_{4} or T_{1} = T_{3} + T_{4}$
or $\frac{p_{1}^{2}}{2 m} = \frac{p_{3}^{2}}{2 m} + \frac{p_{4}^{2}}{2 m}$
or $\frac{p_{1}^{2}}{2 m} = \frac{{(p_{1} - p_{4})}_{1}^{2}}{2 m} + \frac{p_{4}^{2}}{2 m}$ (from eqn.(i))
or $\frac{p_{1}^{2}}{2 m} = \frac{p_{1}^{2} + p_{4}^{2} - 2 p_{1 p_{4}}}{2 m} + \frac{p_{4}^{2}}{2 m} or \frac{p_{1}^{2}}{2 m} = \frac{p_{1}^{2}}{2 m} + \frac{p_{4}^{2}}{2 m} + \frac{p_{4}^{2}}{2 m}$
or $p_{4} (\frac{1}{m} + \frac{1}{M}) = \frac{2 p_{1 p 4}}{2 m} or p_{4} (\frac{1}{m} + \frac{1}{M}) = \frac{2 p_{1}}{m}$
or $p_{4} = (\frac{2 M}{m + M}) p_{1}$
$∴ p_{4}^{2} = {(\frac{2 M}{m + M})}^{2} p_{1}^{2}$ .....(ii)
$∴$ Loss in kinetic energy of neuton $= Δ T_{1} =$ gain in $K . E$ . of deuteron
$Δ T_{1} = T_{4} = \frac{p_{4}^{2}}{2 M}$
Fraction = $\frac{Δ T_{1}}{T_{1}} = \frac{{(\frac{2 M}{m + M})}^{2} \frac{p_{1}^{2}}{2 M}}{\frac{p_{1}^{2}}{2 m}}$
$η = (\frac{2 M}{m + M}) (\frac{m}{M}) = \frac{4 m M}{{(m + M)}^{2}}$
Here $M \approx 2 m$
$∴$ Fraction in $η = \frac{8}{9} = 0.89$
(b) According to conservation priciple of momentum,
${\to p}_{1} + {\to p}_{2} = {\to p}_{3} + {\to p}_{4}$
or $\to p_{1} + 0 = {\to p}_{3} + {\to p}_{4}$
or ${\to p}_{1} - {\to p}_{3}^{2} - 2 p_{1} p_{3} + {\to p}_{4}$
Applying parallelogram law of vectors
$p_{1}^{2} + p_{3}^{2} - 2 p_{1} p_{3} {cos 90}^{\circ} = p_{4}^{2}$
According to conservation principle of kinetic energy
$T_{1} + T_{2} = T_{3} + T_{4}$
or $T_{1} + 0 = T_{3} + T_{4}$
or $\frac{p_{1}^{2}}{2 m} = \frac{p_{3}^{2}}{2 m} + \frac{p_{4}^{2}}{2 m}$
or $\frac{p_{1}^{2}}{2 m} = \frac{p_{3}^{2}}{2 m} + \frac{p_{1}^{2} + p_{3}^{2}}{2 M}$
or $\frac{p_{1}^{2}}{2 m} = \frac{p_{3}^{2}}{2 m} + \frac{p_{1}^{2} + p_{3}^{2}}{2 M}$
or $\frac{p_{1}^{2}}{2 m} = \frac{p_{3}^{2}}{2 m} + \frac{p_{1}^{2} + p_{3}^{2}}{2 M}$
or $\frac{p_{1}^{2}}{2 m} (\frac{1}{m} - \frac{1}{M}) = \frac{p_{3}^{2}}{1} (\frac{1}{m} - \frac{1}{M})$
or $p_{1}^{2} \frac{p_{1}^{2}}{2 m} (\frac{M - m}{m N}) = + p_{3}^{2} (\frac{m + M}{m M})$
or $p_{3}^{2} = (\frac{m - M}{m + M}) p_{1}^{2}$
$∴$ Loss in kinetic energy of neutron is
$Δ T = T_{1} - T_{3}$
$= \frac{p_{1}^{2}}{2 m} - \frac{p_{3}^{2}}{2 m} = \frac{p_{1}^{2} - p_{3}^{2}}{2 m}$
$η = \frac{Δ T}{T_{1}} = \frac{\frac{p_{1}^{2} - p_{3}^{2}}{2 m}}{\frac{p_{1}^{2}}{2 m}}$
$1 - \frac{p_{3}^{2}}{p_{1}^{2}} = 1 - (\frac{M - m}{M + m}) \frac{p_{1}^{2}}{p_{1}^{2}}$
$h = 1 - (\frac{M = m}{M + m}) = \frac{2 m}{M + m} = \frac{2}{3}$

Updated on:21/07/2023

|

Class 12 PHYSICS NUCLEI

Topper's Solved these Questions

Similar Questions

Knowledge Check

A moving neutron collides with a stationary $α$ - particle . The fraction of the kinetic energy lost by the neutron is
A $\frac{16}{25}$
B $\frac{9}{25}$
C $\frac{3}{5}$
D $\frac{2}{5}$
A neutron makes is a head - on elastic collision with a stationary deuteron The fraction energy loss of the neutron in the collision is
A $16 / 81$
B $8 / 9$
C $8 / 27$
D $2 / 3$
A neutron collides head-on and elasticity with an atom of mass number $A$ , which is initially at rest. The fraction of kinetic energy retained by neutron is
A ${(\frac{A}{A + 1})}^{2}$
B ${(\frac{A - 1}{A + 1})}^{2}$
C ${(\frac{A - 1}{A})}^{2}$
D ${(\frac{A + 1}{A - 1})}^{2}$

RESONANCE-NUCLEAR PHYSICS-Advanced level solutions

Home
Ask Doubt
Profile