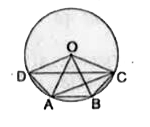
In figure, ABE is a in which AE=BE . Circle passing through A and B intersects AE and BE at D and C respectively. Prove that DC∣∣AB.
We are given, AE=BE,
∴∠EAB=∠EBA→(1)
Also, we know, exterior angle of a cyclic quadrilateral is equal to opposite interior angle.
∴∠EBA=∠EDC→(2)
From (1) and (2),
∠EAB=∠EDC
As both these angles are equal, it implies DC and AB are parallel to each other.
Similar Questions
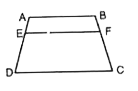
चित्र में यदि EF||DC||AB हो, तो सिद्ध कीजिए की: AEED=BFFC
View SolutionABCD एक समांतर चतुर्भुज है। A,B, और C से होकर जानेवाला वृत्त CD (बढ़ाने पर यदि आवश्यक हो) को E पर प्रतिच्छेद करता है। सिद्ध कीजिए कि AE=AD.z
View SolutionABCD in Figure 11.15 is a parallelogram AE⊥DC and CF⊥AD AB = 16cm, AE = 8m, CF = 10cm But find AD?
View Solutionदी गई आकृति में ABCD एक समलम्ब चतुर्भुज है जिसमे AB∣∣DC है। बिन्दुओं A, B, C एवं D से गुजरते हुए वृत्त का केन्द्र O है। सिद्ध करे कि AD=BC है।
View SolutionIf a line intersects sides AB and AC of a △ABC at D and E respectively and is parallel to BC, prove that ADAB=AEAC (see the given figure).
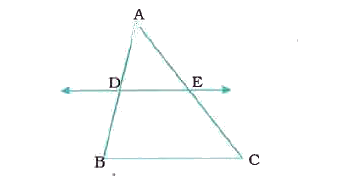
View SolutionA line parallel to BC of a triangle ABC, intersects AB and AC at D and E respectively. Prove that (AD/DB)=(AE/EC).
View Solutionदी गई आकृति में यदि EF ∣∣ DC ∣∣ AB हैं, तो सिद्ध कीजिए कि, AEED=BFFC
View SolutionIn the figure ABCD is a quadrilateral in which AB=AD And BC=DC Prove that angleABC=angleADC Can we say that AE=EC ?
View Solution
