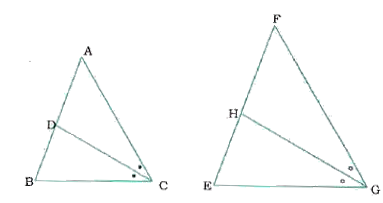
CD and GH are respectively the bisectors of ⌊ACBand⌊EGF such that D and H lie on sidea AB and FE of ΔABCandΔEFG respectively. If ΔABC~ΔFEG, show that.
i] CDGH=ACFG
ii] ΔCDB~ΔHGE
iii] ΔDCA~ΔHGFSolution in Kannada
Step by step video & image solution for CD and GH are respectively the bisectors of lfloorACBandlfloorEGF such that D and H lie on sidea AB and FE of DeltaABCandDeltaEFG respectively. If DeltaABC~DeltaFEG, show that. i] (CD)/(GH)=(AC)/(FG) ii] DeltaCDB~DeltaHGE iii] DeltaDCA~DeltaHGF by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - ZEN PUBLICATIONCHAPTER - TRIANGLESEXERCISE - TEXTUAL EXERCISES (EXERCISE 2.4)
9 Videos
- TRIANGLESBOOK - ZEN PUBLICATIONCHAPTER - TRIANGLESEXERCISE - TEXTUAL EXERCISES (EXERCISE 2.5)
17 Videos
- TRIANGLESBOOK - ZEN PUBLICATIONCHAPTER - TRIANGLESEXERCISE - TEXTUAL EXERCISES (EXERCISE 2.2)
9 Videos
- SURFACE AREAS AND VOLUMESBOOK - ZEN PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - ZEE ADDITIONAL QUESTIONS -HOTS [HIGHER ORDER THINKING SKILLS]-QUESTIONS
11 Videos
Similar Questions
Let ΔABC~ΔDEF and their areas be , respectively , 64cm2and121cm2 . If EF = 15.4 cm, find BC
View SolutionSides of triangles are given below. Determine which of them are right triangles.
In case of a right triangle , write the length of its hypotenuse.
7cm, 24 cm, 25 cm
View SolutionE and F are points on the sides PQ and PR respectively of a ΔPQR. For the following cases, state whether EF||QR.

i] PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm, and FR = 2.4 cm.
ii] PE = 4 cm, QE = 4.5 cm, PF = 8 cm, RF = 9 cm
iii] PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm, and PF = 0.36 cm.
View SolutionA sector of a circular is of radius 12 cm and angle 120∘. It is rolled up so that two bounding radii are joined together to form a cone. Find the volume of the cone.
View SolutionCD और GH क्रमशः ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिन्दु D और H क्रमशः ΔABC और ΔEFG की भुजाओं AB और FE पर स्थित हैं । यदि ΔABC~ΔFEG तो दर्शाइए कि
(i) CDGH=ACFG
(ii) ΔDCB~ΔHGE
(iii) ΔDCA~ΔHGF
View SolutionCD and GH are the bisectors of ∠ACB and ∠EGF respectively. If D lies on AB of ΔABC and H lies on EF of ΔEFG and if ΔABC~ΔEFG, then prove that (a) CDGH=ACFG, (b)ΔDCB~ΔHGE, (c)ΔDCA~ΔHGF
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
CDGH=ACFG
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
ΔDCB~ΔHGE
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
ΔDCA~ΔHGF
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
CDGH=ACFG
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
ΔDCB~ΔHGE
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
ΔDCA~De<HGF
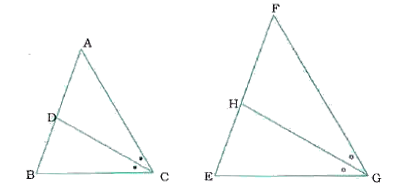
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG, show that :
CDGH=ACFG
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG, show that :
ΔDCB~ΔGHE
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG, show that :
ΔDCA~ΔHGF

View Solution
