दी आकृति में , AB और PQ एक वृत्त के लंबवत व्यास है जिसका केंद्र O और त्रिज्या OA = 7 सेमी है । छायांकित भाग का क्षेत्रफल ज्ञात कीजिए ।

Video Solution

Text Solution

Verified by Experts

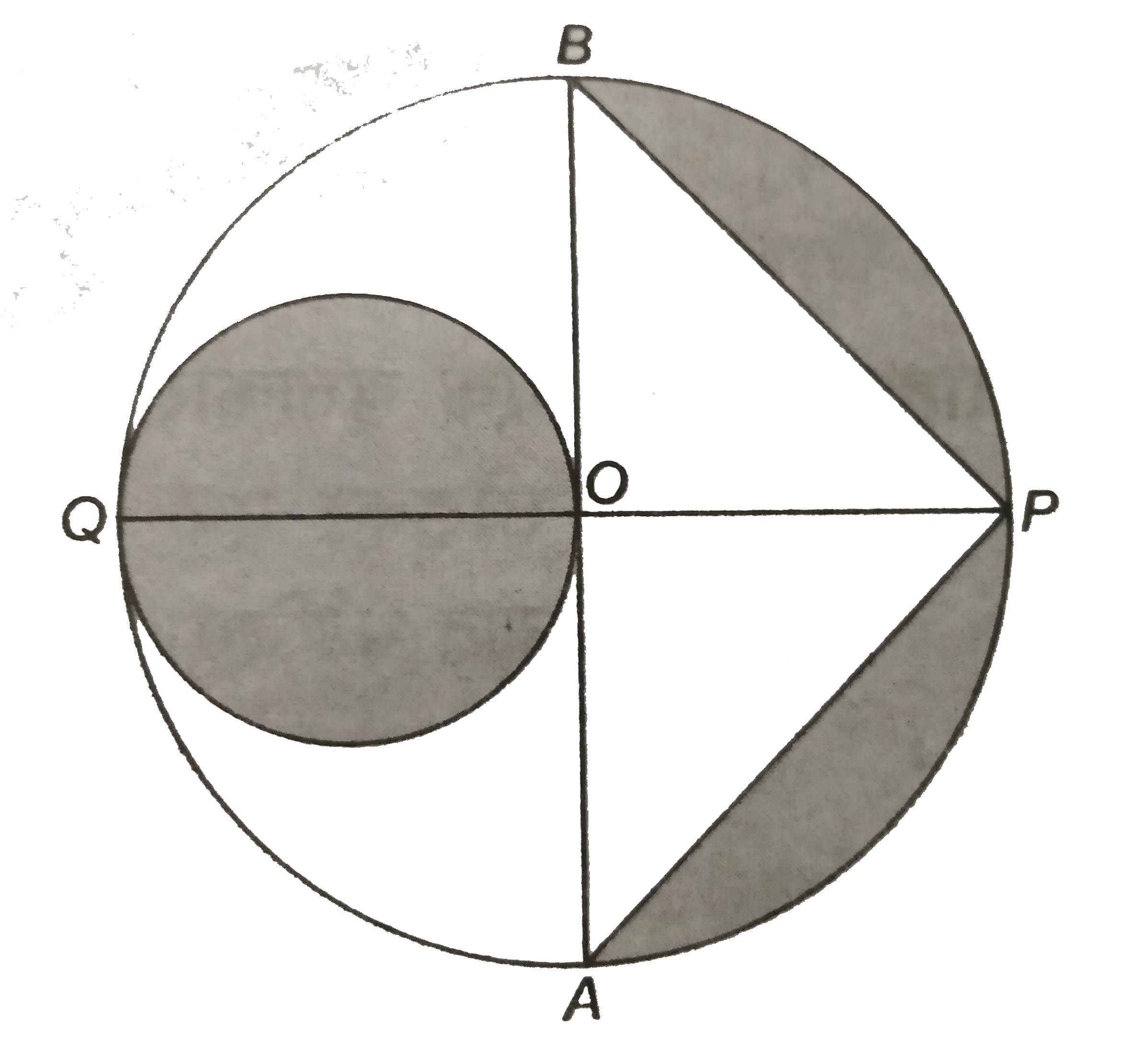
छोटे वृत्त का व्यास = OQ = OA = 7 सेमी
त्रिज्या $(r) = \frac{7}{2} = 3.5$ सेमी
छोटे वृत्त की क्षेत्रफल $= π r^{2}$
$= \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} {सेमी}^{2}$
$= \frac{77}{2} {सेमी}^{2} = 38.5 {सेमी}^{2}$
अर्द्धवृत्त APBOA का क्षेत्रफल $= \frac{1}{2} π r_{1}^{2}$ ( जहाँ $r_{1}$ = अर्द्धवृत्त APBOA की त्रिज्या )
$= \frac{1}{2} \times \frac{22}{7} \times 7 \times 7 {सेमी}^{2} = 77 {सेमी}^{2}$
$Δ A P B$ का क्षेत्रफल $= \frac{1}{2} \times A B \times O P = \frac{1}{2} \times 14 \times 7 = 49 {सेमी}^{2}$
छायांकित भाग APB का क्षेत्रफल
= अर्द्धवृत्त का क्षेत्रफल - $Δ A P B$ का क्षेत्रफल
$= 77 {सेमी}^{2} - 49 {सेमी}^{2} = 28 {सेमी}^{2}$
अब , छायांकित भाग का कुल क्षेत्रफल = छोटे वृत्त ( छायांकित ) का क्षेत्रफल + छायांकित भाग APB का क्षेत्रफल
$= 38 .5 + 28 = 66.5 {सेमी}^{2}$

|

Updated on:21/07/2023

Class 10 MATHS AREAS RELATED TO CIRCLES

Topper's Solved these Questions

Similar Questions

NOOTAN HINDI-वृत्तों से समबन्धित क्षेत्रफल -विविध प्रश्नावली ( बहुविकल्पीय प्रश्न )

Home
Ask Doubt
Profile