Question

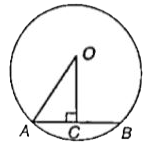
In a circle centred at O, AB is a chord and C is any point on AB such that OC is perpendicular to AB. If the radius of the circle is 10 cm and OC = 6 cm, then the length of the chord is:
एक वृत्त में O केंद्र है , AB एक जीवा है और C, AB पर कोई बिंदु है जैसे OC, AB पर लंबवत है। यदि वृत्त की
त्रिज्या 10 सेमी और OC = 6 सेमी है, तो जीवा की लंबाई ज्ञात करे |

Options

A. 8
B. 12
C. 4
D. 16

Explanation

To find the length of the chord AB in the given circle, we can follow these steps:

Step 1: Understand the Geometry
We have a circle with center O, a chord AB, and a point C on the chord such that OC is perpendicular to AB. Given the radius of the circle (OA = OB) is 10 cm and OC = 6 cm.

Step 2: Apply the Pythagorean Theorem
In the right triangle OAC, we can apply the Pythagorean theorem. According to the theorem:
\( OA^2 = OC^2 + AC^2 \)
Where:
- OA = radius of the circle = 10 cm
- OC = 6 cm
- AC = half the length of the chord AB

Step 3: Substitute the Known Values
Substituting the known values into the equation:
\( 10^2 = 6^2 + AC^2 \)
\( 100 = 36 + AC^2 \)

Step 4: Solve for AC
Now, isolate AC^2:
\( AC^2 = 100 - 36 \)
\( AC^2 = 64 \)
Taking the square root of both sides gives:
\( AC = \sqrt{64} = 8 \text{ cm} \)

Step 5: Find the Length of the Chord AB
Since C is the midpoint of the chord AB, the full length of the chord AB is:
\( AB = AC + BC = AC + AC = 2 \times AC = 2 \times 8 = 16 \text{ cm} \)

Conclusion
The length of the chord AB is 16 cm.

---