PQRS is a parallelogram and its area is 300 cm2. Side PQ is extended to X such that PQ=QX. If XS intersects QR at Y, then what is the area (in cm2) of triangle SYR?
PQRS एक समांतर चतुर्भुज है तथा 300 से.मी.2 है। भुजा को तक इस तरह बढाया गया कि PQ=QX है। यदि XS, QR को Y पर काटता है, तो त्रिसुज SYR का क्षेत्रफल (से.मी.2 में) क्या हैं?
A)75
B)50
C)120
D)100
To solve the problem, we will follow these steps:
Step 1: Understand the Parallelogram
We have a parallelogram PQRS with an area of 300 cm². The sides PQ and SR are parallel, and the sides PS and QR are also parallel.
Step 2: Extend Side PQ
We extend side PQ to point X such that PQ = QX. This means that the length of QX is equal to the length of PQ.
Step 3: Identify the Intersection
The line segment XS intersects QR at point Y.
Step 4: Analyze the Triangles
Since PQ = QX, we can see that triangle QXS is similar to triangle QSR. The reason is that they share angle Q, and the angles at points S and R are equal because they are alternate interior angles (due to the parallel lines).
Step 5: Area Relationships
Let the area of triangle QSR be A. Since triangles QXS and QSR are similar and the ratio of their corresponding sides is 1:2 (because QX is equal to PQ), the area of triangle QXS will be 1/4 of the area of triangle QSR. Therefore, if the area of triangle QSR is A, then the area of triangle QXS is A/4.
Step 6: Total Area of Parallelogram
The area of parallelogram PQRS can be expressed as the sum of the areas of triangles QSR and QXS:
Area of PQRS=Area of QSR+Area of QXS
300=A+A4
Step 7: Solve for A
To solve for A, we can combine the terms:
300=A+A4
300=4A+A4
300=5A4
Multiplying both sides by 4 gives:
1200=5A
Dividing both sides by 5 gives:
A=240 cm2
Step 8: Area of Triangle SYR
The area of triangle SYR is equal to the area of triangle QSR minus the area of triangle QXS:
Area of SYR=A−A4
Area of SYR=240−60=180 cm2
Final Answer
Thus, the area of triangle SYR is 180 cm².
---
We have a parallelogram PQRS with an area of 300 cm². The sides PQ and SR are parallel, and the sides PS and QR are also parallel.
We extend side PQ to point X such that PQ = QX. This means that the length of QX is equal to the length of PQ.
The line segment XS intersects QR at point Y.
Since PQ = QX, we can see that triangle QXS is similar to triangle QSR. The reason is that they share angle Q, and the angles at points S and R are equal because they are alternate interior angles (due to the parallel lines).
Let the area of triangle QSR be A. Since triangles QXS and QSR are similar and the ratio of their corresponding sides is 1:2 (because QX is equal to PQ), the area of triangle QXS will be 1/4 of the area of triangle QSR. Therefore, if the area of triangle QSR is A, then the area of triangle QXS is A/4.
The area of parallelogram PQRS can be expressed as the sum of the areas of triangles QSR and QXS:
Area of PQRS=Area of QSR+Area of QXS
300=A+A4
To solve for A, we can combine the terms:
300=A+A4
300=4A+A4
300=5A4
Multiplying both sides by 4 gives:
1200=5A
Dividing both sides by 5 gives:
A=240 cm2
The area of triangle SYR is equal to the area of triangle QSR minus the area of triangle QXS:
Area of SYR=A−A4
Area of SYR=240−60=180 cm2
Thus, the area of triangle SYR is 180 cm².
Topper's Solved these Questions
Similar Questions
PQR is a right angled triangle in which PQ = QR. If the hypotenuse of the triangle is 20 cm, then what is the area (in cm2) of the triangle PQR?
PQR एक समकोण त्रिभुज है जिसमें PQ = QR है। यदि त्रिभुज का कर्ण 20 से.मी. हैं त्रिभुज PQR का क्षेत्रफल (से.मी.2 में) क्या हैं?
View SolutionIn the given figure, PQR is a quadrant whose radius is 7cm.A circle is incribed in the quadrant as shown in the figure.What is the area (in cm2) of the circle?
दी गई आकृति में, PQR एक वृत्त-खण्ड है जिसकी त्रिज्या 7 से.मी. है। जेसा कि आकृति में दर्शाया गया है कि वृत्त-खण्ड में एक वृत्त को अंकित किया गया हें वृत्त का क्षेत्रफल (से.मी.2 में) क्या है?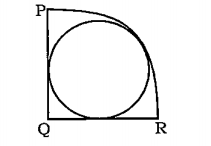
View Solution
Knowledge Check
In a triangle PQR, PX bisects QR. PX is the angle bisector of angle P. If PQ=12 cm and QX=3 cm, then what is the area (in cm2) of triangle PQR?
A12√3B8√15C18√2D9√15PQR is a right angled triangle at Q in which PQ = QR. If the hypotenuse of the triangle is 20 cm, then what is the area (incm2) of the triangle PQR ?
A100√2B100C50√2D50PQRS is a rectangle, A, B, C and D are the mid points of sides PQ, QR, RS and PS respectively. If area of ΔPQR is 48 cm2, then what is the area (in cm2) of ΔBCD?
A24B6C16D12
PQ and RS are two chords, of a circle. PQ =20 cm, RS =48 cm and PQ is parallel to RS. If the distance between PQ and RS is 34 cm, then what is the area (in cm2) of the circle?
PQ तथा RS एक वृत्त की 2 जीवाएं हैं। PQ=20 सेमी., RS =48 सेमी. तथा PQ,RS के समानान्तर है। यदि PQ तथा RS के मध्य दूरी 34 सेमी. है, तो वृत्त का क्षेत्रफल (सेमी.2) क्या है?
View SolutionIn the given figure, PQRS is a square of side 8 cm. ∠PQO=60∘. What is the area (in cm2) of the triangle POQ?
दी गई आकृति में, PQRS 8 से.मी. भुजा वाला एक वर्ग है। ∠PQO=60∘ है। त्रिभुज POQ का क्षेत्रफल (से.मी2 में) क्या है?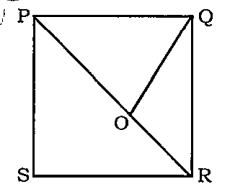
View SolutionIf the height of an equilateral triangle is 12 cm, then what is the area of the triangle?
यदि एक समबाह त्रिभुज की ऊंचाई 12 सेमी है, तो त्रिभुज का क्षेत्रफल कितना है?
View SolutionIn the given figure, PQR is an equilateral triangle with side as 12cm. S and T are the mid points of the sides PQ and PR respectively. What is the area (in cm2) of the shaded region?
दी गई आकृति में PQR एक समबाहु त्रिभुज है जिसकी भुजा 12 से.मी. हैं। S तथा T क्रमशः भुजा PQ तथा PR के मध्य बिन्दु है। छायांकित भाग का क्षेत्रफल (से.मी.2 में) क्या है?
View SolutionIn the given figure PQRSTU is a regular hexagon of side 12 cm. what is the area (in cm2) of triangle SQU?
दी गई आकृति में, PQRSTU एक समषट्भुज है जिसकी भुजा 12 से.मी. हे। त्रिभुज SQU का क्षेत्रफल (से.मी.2 में) क्या है?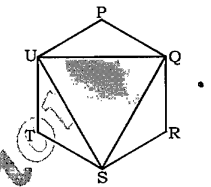
View Solution
