में, भुजाओं AB तथा BC के मध्य-बिंदु क्रमशः P तथा Q है और AP का मध्य-बिंदु R है। सिद्ध कीजिए कि
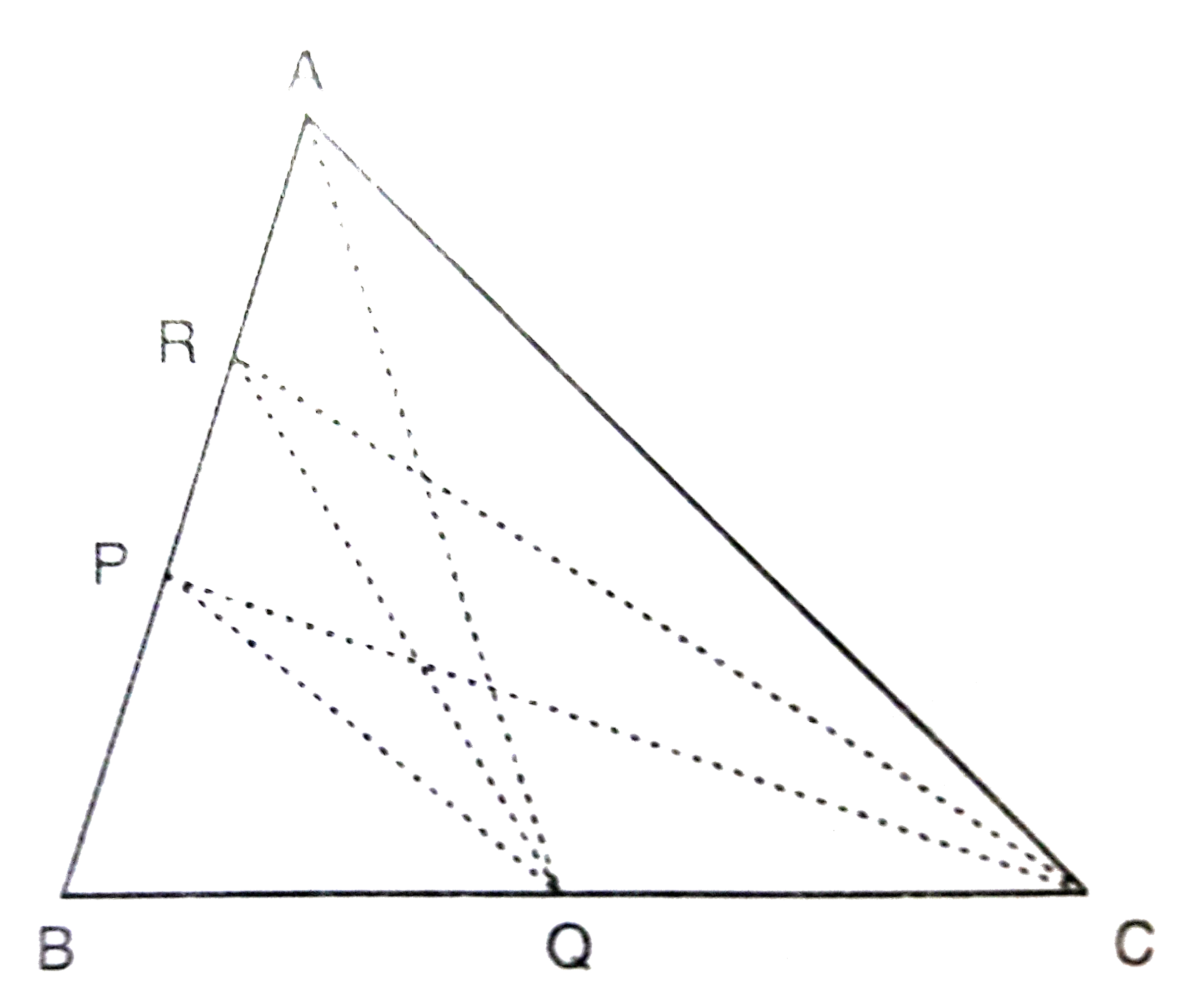
हम जानते है कि किसी त्रिभुज की माध्यिका उसे समान क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है।
चूँकि की एक माध्यिका है।
...( i)
की एक माध्यिका है।
...(ii)
(i ) तथा (ii ) से हम स्पष्ट है कि
...(iii)
चूँकि के एक माध्यिका है ।
...(iv)
(iii ) तथा (iv ) से,
...(v)
(ii ) चूँकि QP और QR क्रमशः और QAP के माध्यिकाएँ है।
...(vi)
तथा ...(vii)
(vi ) तथा (vii ) से
...(viii)
(v ) तथा (viii ) से,
...(viii)
(iii ) चूँकि की एक माध्यिका है।
...(ix)
चूँकि की एक माध्यिका है।
[(ix) से]
Topper's Solved these Questions
- BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - अति लघुत्तरात्मक प्रश्न9videos
समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - बहु विकल्पीय प्रश्न20videos
समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 15.24videos
समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - RD SHARMACHAPTER - संख्यिकीय आंकड़ों का आलेखीय निरूपण EXERCISE - बहु विकल्पीय प्रश्न8videos
संख्यिकीय आंकड़ों का आलेखीय निरूपण
- BOOK - RD SHARMACHAPTER - सर्वांगसम त्रिभुजेंEXERCISE - बहु विकल्पीय प्रश्न17videos
सर्वांगसम त्रिभुजें
Similar Questions
यदि ABC व BDE दो समबाहु त्रिभुज इस प्रकार है कि बिंदु D भुजा BC का मध्य बिंदु है, तो त्रिभुज ABC और त्रिभुज BDE के क्षेत्रफल का अनुपात ज्ञात करो।
02:48View Solutionयदि दो समांतर चतुर्भुजों का एक ही आधार है और समान समांतर रेखाओं के बीच स्थित है तो उनके क्षेत्रफलों के बीच क्या अनुपात होगा :
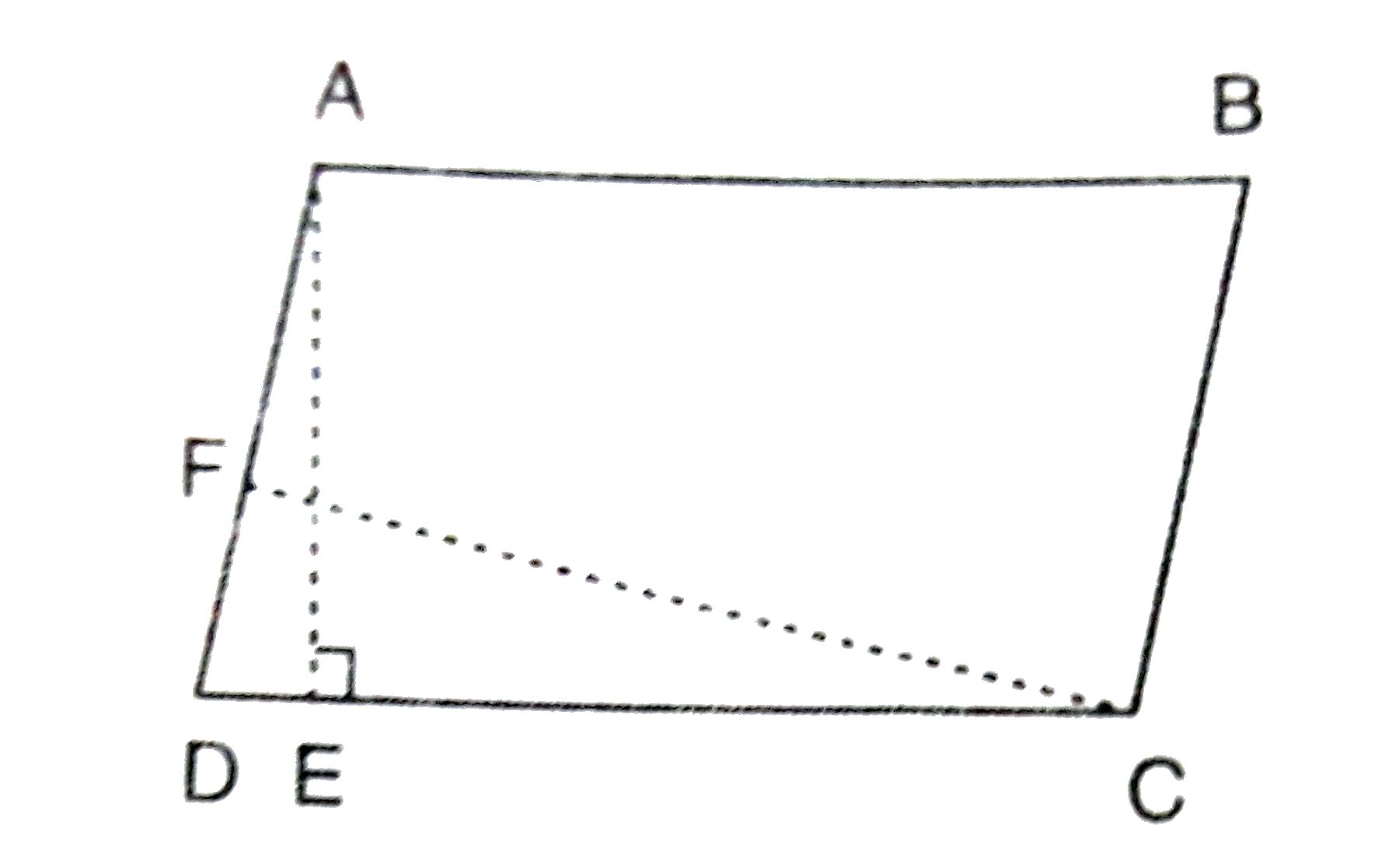
View Solutionचित्र में , ABCD एक समान्तर चतुर्भुज है। AE⊥DC तथा CF⊥AD । यदि AB = 16 सेमी, AE = 8 सेमी तथा CF = 10 सेमी , तो AD का मान ज्ञात कीजिये ।
 11:03View Solution
11:03View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
04:36View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
10:39View SolutionIf ΔABC~ΔPQR with BCQR=13,then ar(ΔPRQ)ar(ΔBCA) is equal to
View SolutionIn the figure, ABC and BDE are two equilateral triangle such that D is the mid-point of BC. If AE intersects BC at F, show that:
(i) ar(ΔBDE)=14ar(ΔABC) (ii) ar(ΔBDE)=12ar(ΔBAE)
(iii) ar(ΔABC)=2ar(ΔBEC) (iv) ar(ΔBFE)=ar(ΔAFD)
(v) ar(ΔBFE)=2ar(ΔFED) (vi) ar(ΔFED)=18ar(ΔAFC)
 03:03View Solution
03:03View Solutionयदि ΔABC की माध्यिकायें बिंदु G पर प्रतिच्छेद करती है, तो सिद्ध कीजिए कि
ar(ΔAGB)=ar(ΔAGC)=ar(ΔBGC)=13ar(ΔABC)17:01View Solutionयदि ABCD एक समांतर चतुर्भुज है, तो सिद्ध कीजिए कि
ar(ΔABD)=ar(ΔBCD)=ar(ΔABC)=ar(ΔACD)=12ar(||gmABCD)02:35View SolutionΔABC में, भुजाओं AB तथा AC पर क्रमशः बिंदु L तथा M इस प्रकार है कि LM ।। BC सिद्ध कीजिए कि
(i) ar(ΔLCM)=ar(ΔLBM)
(ii) ar(ΔLBC)=ar(ΔMBC)
(iii) ar(ΔABM)=ar(ΔACL)
(iv) ar(ΔLOB)=ar(ΔMOC)View SolutionP और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य बिंदु है तथा R रेखाखण्ड AP का मध्य बिंदु है |दर्शाइए
(i)ar(PQR)=12ar(ARC)
(ii)ar(RQC)=38ar(ABC)01:34View Solutionयदि ΔABC~ΔPQR तथा BC=5QR तो ar(ΔABC):ar(ΔPQR) है
04:48View SolutionP और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य-बिन्दु है तथा R रेखाखण्ड AP का मध्य-बिन्दु है। दर्शाइए कि :
(i) ar(PRQ)=12ar(ARC)
(ii) ar(RQC)=38ar(ABC)
(iii) ar(PBQ)=ar(ARC)06:00View SolutionΔABC~ΔPQR, AB:PQ=3:4 then ar ΔABC: ar ΔPQR=……
05:07View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid point at AP, show that
(i) ar (PQR) = 12 ar (ARC)
(ii) ar (RQC) = 38 ar (ABC)
(iii) ar (PBQ) = ar (ARC)02:50View Solution

