If f(x)=|x−3|+2 , evalute limx→3+f(x)−f(3)x−3 and limx→3−f(x)−f(3)x−3
Hence examine the differentiability of f(x) at x = 3 . Solution in Bengali
The correct Answer is:1 and −1 , not differentiable
Step by step video, text & image solution for If f(x) = |x-3| + 2 , evalute lim_(x to 3 + ) (f(x)-f(3))/(x-3) and lim_(x to 3 - ) (f(x)-f(3))/(x-3) Hence examine the differentiability of f(x) at x = 3 . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIATIONBOOK - CHHAYA PUBLICATIONCHAPTER - DIFFERENTIATIONEXERCISE - Long Answer Type Questions
23 Videos
- DIFFERENTIATIONBOOK - CHHAYA PUBLICATIONCHAPTER - DIFFERENTIATIONEXERCISE - Sample Questions for competitive Exams ( A Mulitple Correct Answers type )
5 Videos
- DIFFERENTIATIONBOOK - CHHAYA PUBLICATIONCHAPTER - DIFFERENTIATIONEXERCISE - Very short Answer Type Questions
38 Videos
- DIFFERENTIAL EQUATIONS OF THE FIRST ORDER AND FIRST DEGREE BOOK - CHHAYA PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONS OF THE FIRST ORDER AND FIRST DEGREE EXERCISE - E ASSERTION-REASON TYPE
2 Videos
- DIRECTION COSINES AND DIRECTION RATIOSBOOK - CHHAYA PUBLICATIONCHAPTER - DIRECTION COSINES AND DIRECTION RATIOSEXERCISE - Assertion-Reason Type
2 Videos
Similar Questions
Find from the first principle, the derivatives of the following functions w.r.t. x :
sin(x2+1)
View SolutionIf y=x4−x2+1x2+√3x+1 and dydx=ax+b , then a - b = ?
View SolutionDefine the derivative of a function f(x) at an arbitrary point x in its domain of definition.
View SolutionLet y(x) be a solution of xdy+ydx+y2(xdy−ydx)=0 satsfying y(1)=1
Statement -I : The range of y(x) has exactly two points.
Statement0-II : The constant of integration is zero.
View SolutionConsider the points A(0, 0, 0), B(2, 0, 0), C(1,√3,0) and D(1,1√3,2√2√3)
Statement - I : ABCD is a square.
Statement - II : |AB|=|BC|=|CD|=|DA|.
View SolutionThe graph of y = f(x) is as shown in the following figure.
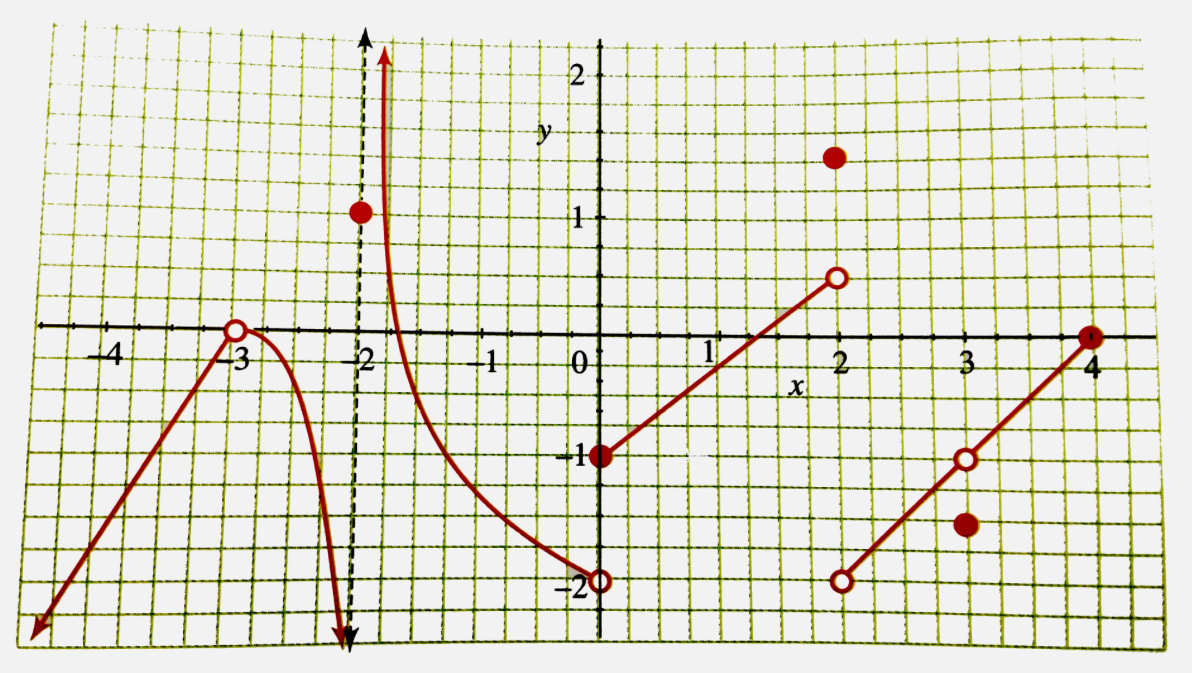
Find the following values
(i)f(−3) (ii)f(−2) (iii)f(0)
(iv)f(2) (v)f(3) (vi)limx→−3f(x)
(vii)limx→0f(x) (viii)limx→2f(x) (ix)limx→3f(x)
(x)limx→2−f(x) (ξ)limx→−2+f(x) (xii)limx→0−f(x)
(x iii) limx→0+f(x)
View SolutionIf f : R → R is defined by f (x) f(x) = [ x -3] + | x -4| for x ∈ R
then limx→3f(x) is equal to
View SolutionFind limx→3f(x),wheref(x)=|x−3|x−3,x≠3.
View SolutionFor a differentiable function f(x), if f'(2)=2andf'(3)=1, then the value of limx→0f(x2+x+2)−f(2)f(x2−x+3)−f(3) is equal to
View SolutionEvaluate limx→3x2−9x−3 if it exists by finding f(3−) and f(3+)
View SolutionVerify the existence of limx→3f(x), where f(x)={|x−3|x−3forx≠30forx=3
View SolutionLet f:R→[0,∞) be such that limx→3f(x) exists and limx→3(f(x))2−4√|x−3|=0. Then limx→3f(x) equals
View SolutionThe graph of y = f(x) is as shown in the following figure.

Find the following values
(i)f(−3) (ii)f(−2) (iii)f(0)
(iv)f(2) (v)f(3) (vi)limx→−3f(x)
(vii)limx→0f(x) (viii)limx→2f(x) (ix)limx→3f(x)
(x)limx→2−f(x) (ξ)limx→−2+f(x) (xii)limx→0−f(x)
(x iii) limx→0+f(x)
View Solutionlimx→af(x)−f(a)x3−a3=……………
View SolutionConsider f(x)={2x+3x≤2x+2kx>2
Evalute limx→2+f(x)
View Solution
