The force constant of a linear harmonic oscillator is 10 N/m. If is P.E. at a point in its path is 0.05J, its corresponding displacement is
1 metre
0.5 m
0.25 m
0.1 m
The correct Answer is:D
P.E. =12kx2
∴5100=12×10×x2∴x=0.1m
Topper's Solved these Questions
Similar Questions
When the displacement of a simple harmonic oscillator is half of its amplitude, its potential energy is 3J. Its total energy is
View SolutionThe variation of potential energy (U) of a simple harmonic oscillator is as shown. Then force constant of the system is (PE is in joules, displacement 'x' is in mm)
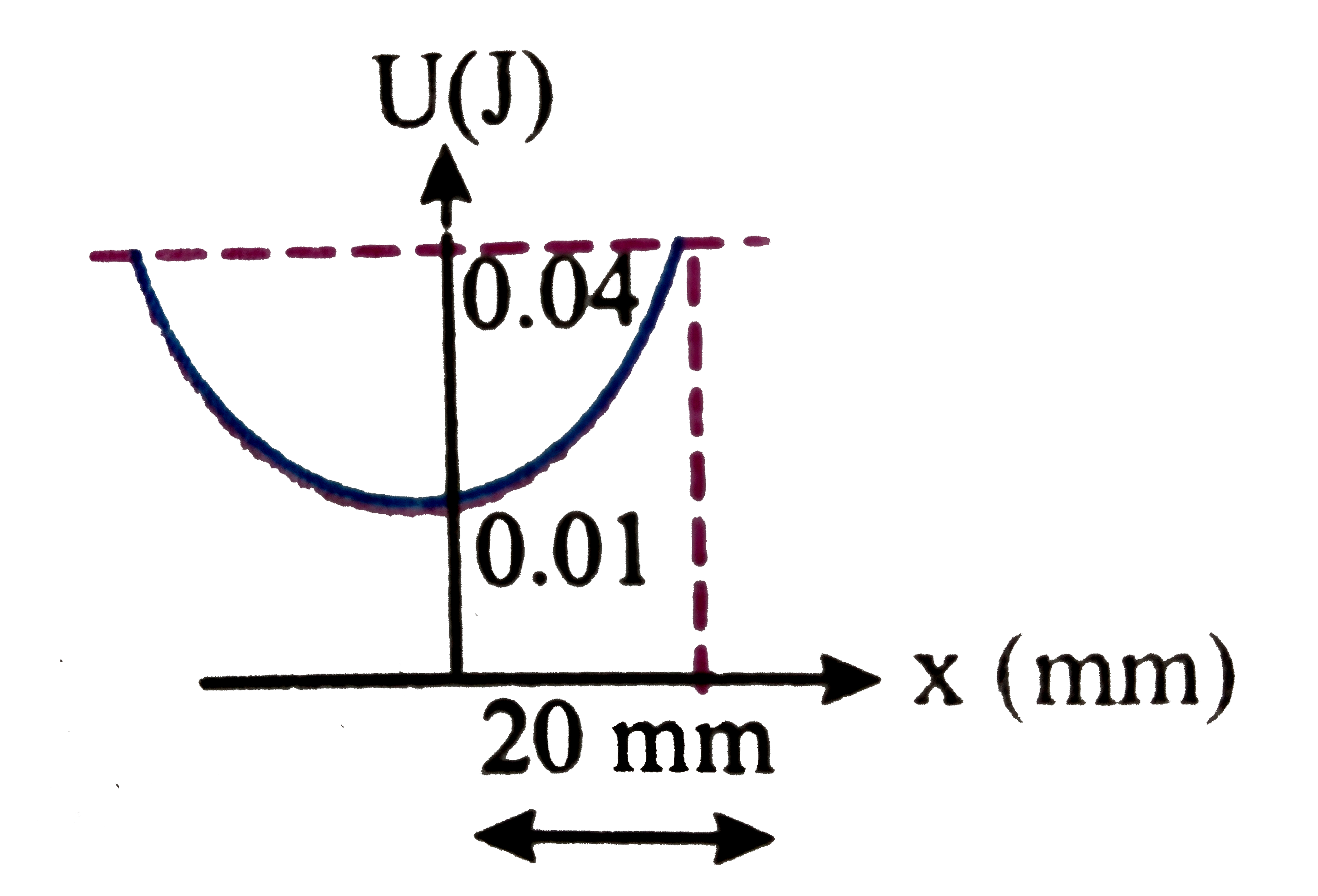
View Solution
Knowledge Check
The force constant of a simple harmonic oscillator is 3×106N/m, amplitude 0.02 m has a total energy of 1250 J
AMaximum potential energy is 650 JBMaximum kinetic energy is 600 JCMaximum kinetic energy is 700 JDMaximum potential energy is 450 JWhen the displacement of a linear harmonic oscillator is 1/3 of its amplitude, the ratio of its total energy to its potential energy is
A3B4C9D19A linear harmonic oscillator of force constant 106N/m and amplitude 2 cm has
Aa maximum P.E. of 100 JouleBa maximum K.E. of 150 JuleCa total energy of 200 JDa total energy of 300 J
A spring executes SHM with mass of 10 kg attached to it. The force constant of spring is 10 N/m. If at any instant its velocity is 40 cm/sec, the displacement will be (where amplitude is 0.5 m )
View SolutionThe maximum potential energy of a simple harmonic oscilator is Umax. The the P.E. of the oscillator when it is half way to its end point is
View SolutionThe displacement of a simple harmonic oscillator is, x = 5 sin (πt/3)m. Then its velocity at t = 1 s, is
View SolutionA spring executes SHM with mass off 10 kg attached to it. The force constant of spring is 10N/m. If at any instant its velocity is 40cm/s , the displacement will be (where amplitude is 0.5m)
View SolutionThe acceleration of a simple harmonic oscillator is 1m/s2 when its displacement from mean position is 0.5 m. Then its frequency of oscillation is
View Solution
