Find the area of the smaller region bounded by the ellipse $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ and the line $\frac{x}{3} + \frac{y}{2} = 1$

$\frac{1}{2} (π - 2)$ sq. units

$\frac{3}{2} (π - 2)$ sq. units

$\frac{5}{4} (π - 2)$ sq. units

$\frac{2}{3} (π - 2)$ sq. units

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Answer

Step by step video, text & image solution for Find the area of the smaller region bounded by the ellipse (x^2)/9+(y^2)/4=1 and the line x/3+y/2=1 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS INTEGRALS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Find the area of the region bounded by the ellipse $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ in fourth quadrant.
A $\frac{3 π}{4}$ sq units
B $\frac{3 π}{2}$ sq units
C $\frac{5 π}{2}$ sq units
DNone of these
Question 2 - Select One
Find the area of the region bounded by the ellipse $\frac{x^{2}}{4} + \frac{y^{2}}{9} = 1 .$

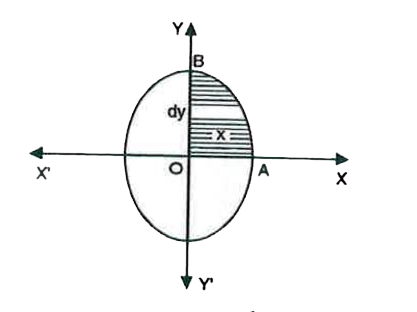A $10 π$
B $11 π$
C $12 π$
D $13 π$
Question 3 - Select One
The area of the smaller region bounded by the circle $x^{2} + y^{2} = 1$ and the lines $| y | = x + 1$ is
A $(π - 2) / 4$
B $(π - 2) / 2$
C $(π + 2) / 2$
DNone of these

TARGET PUBLICATION-APPICATIONS OF DEFINITE INTEGRAL-CRITICAL THINKING

Home
Ask Doubt
Profile

Find the area of the smaller region bounded by the ellipse x29+y24=1 and the line x3+y2=1

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

Find the area of the region bounded by the ellipse x29+y24=1 in fourth quadrant.

Find the area of the region bounded by the ellipse x24+y29=1.

The area of the smaller region bounded by the circle x2+y2=1 and the lines |y|=x+1 is

TARGET PUBLICATION-APPICATIONS OF DEFINITE INTEGRAL-CRITICAL THINKING

Find the area of the smaller region bounded by the ellipse $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ and the line $\frac{x}{3} + \frac{y}{2} = 1$

Find the area of the region bounded by the ellipse $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ in fourth quadrant.

Find the area of the region bounded by the ellipse $\frac{x^{2}}{4} + \frac{y^{2}}{9} = 1 .$

The area of the smaller region bounded by the circle $x^{2} + y^{2} = 1$ and the lines $| y | = x + 1$ is