Two satellites of same mass are launched in the same orbit round the earth so as to rotate opposite to each other. They soon collide inelastically and stick together as wreckage. Obtain the total energy of the system before and just after the collision. Describe the subsequent motion of the wreckage.
In case of satellite motion, energy of a satellite in an orbit is given by E=−GMm2r So the total energy of the system before collision Ei=E1+E2=2E=−GMmr
As the satellites of equal mass are moving in opposite direction and collide inelastically, the velocity of wreckage just after collision, by conservation of linear momentum will be mv−mv=2mv, i.e.,v=0 i.e., just after collision wreckage comes to rest in the orbit. so energy of the wreckage just after collision will be totally potential and will be EP=−GM(2m)r=−2GMmr
And as after collision the wreckage comes to rest in the orbit, it will move along the radius towards the earth under is gravity.
Topper's Solved these Questions
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - C.U.Q
220 Videos
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL I(C.W.)
51 Videos
- FRICTIONBOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I
6 Videos
- KINETIC THEORY OF GASESBOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)
52 Videos
Similar Questions
_E01_109_Q01.png)
Consider two satellites A and B of equal mass m, moving in the same circular orbit of radius r around the earth E but in opposite sense of rotation and therefore on a collision course (see figure)
(i). In terms of G,Me m and r find the total mechanical energy EA+EB of the two satellite plus earth system before collision
(ii). If the collision is completely inelastic so that wreckage remains as one piece of tangled material (mass=2m) find the total mechanical energy immediately after collision.
(iii). Describe the subsequent motion of the wreckage.
View SolutionConsider two satellites A and B of equal mass, moving in the same circular orbit of radius r around the earth but in the opposite sense and therefore a collision occurs.
(a) Find the total mechanical energy EA+EB of the two satellite-plus-earth system before collision.
(b) If the collision is completely inelastic, find the total mechanical energy immediately after collision. Describe the subsequent motion of the combined satellite.
View Solution
Knowledge Check
Two satellite of same mass are launched in the same orbit of radius r around the earth so as to rotate opposite to each other. If they collide inelastically and stick together as wreckage, the total energy of the system just after collision is
A−2GMmrB−GMmrCGMm2rDzeroTwo identical satellite are kept in the same orbit around the earth to move in opposite directions. If they collide and stick together after some time
Athe satellites fly away from the earth into spaceBthey fall freely towards the earthCthey continue to move in the same orbitDthey moves into an orbit at a higher levelTwo oppositely rotating satellities of same are launched in the same orbit round the earth. The collide idealistically. What is the ratio of gravitational potential energy before and after collistion?
A2B12C√2D1√2
Two objects each of mass 5 kg are moving in the same straight line but in the opposite direction towards each other with some speed of 3 m/s. They stick to each other after collision. What will be the velocity of the combined object after collision?
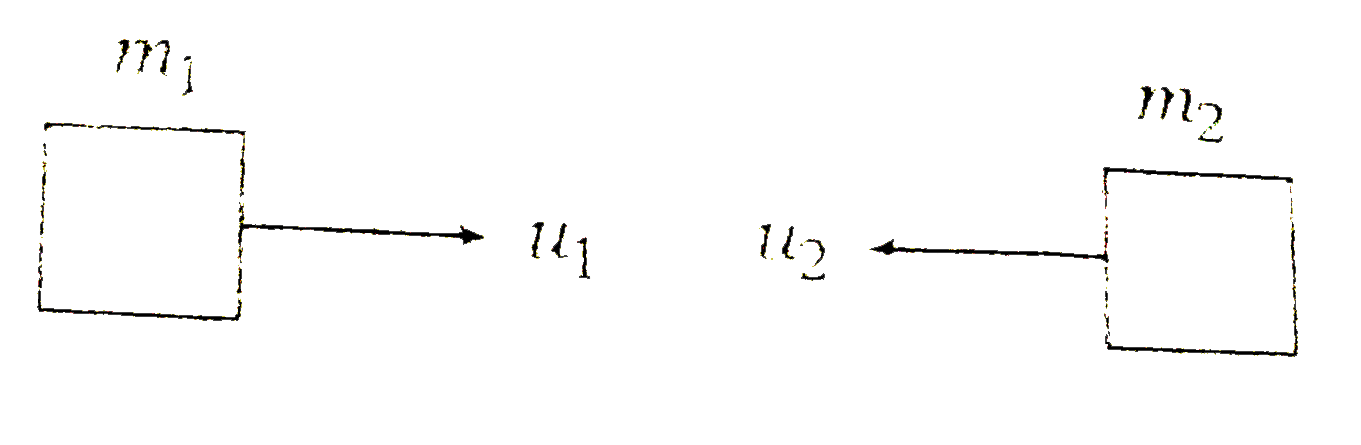
View SolutionTwo object, each of mass 1.5kg, are moving in the same straight line but in opposite directions, The velocity of each object is 2.5ms−1 before the collision during which they stick together. What will be the velocity of the combined object after collision?
View SolutionTwo satellites of same mass are orbiting round the earth at heights of r1 and r2 from the centre of earth. Their kinetic energies are in the ratio of :
View SolutionTwo satellites of same mass m are revolving round of earth (mass M) in the same orbit of radius r. Rotational directions of the two are opposite therefore, they can collide. Total mechanical energy of the system (both satallites and earths) is (m<<M) :-
View SolutionA satellite of mass M is in a circular orbit of radius R about the centre of the earth. A meteorite of the same mass, falling towards the earth, collides with the satellite completely inelastically. The speeds of the satellite and the meteorite are the same, just before the collision. The subsequent motion of the combined body will be:
View Solution
