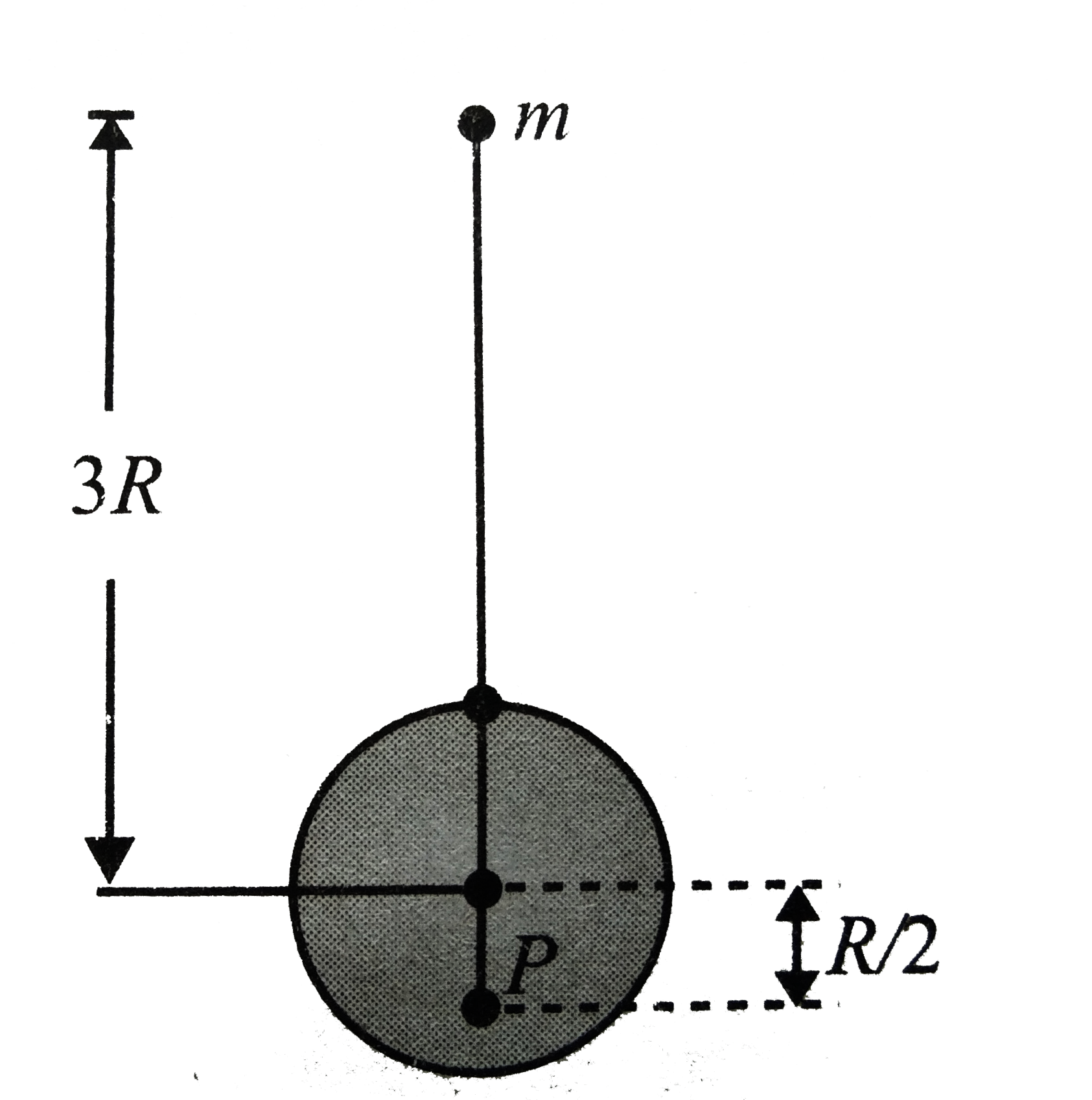
A point of mass m is released from rest at a distance of 3R from the cente of a then walled hollow spehre of radius R and mass M as shown. The hollow sphere is fixed in position and the motion is due to only gravitational attraction of the hollow sphere. There is a very small hole in the hollow sphere through which the point mass falls as shown. Then the velocity of point mas when it passes through point P at distance R/2 from the centre of the sphere is

The correct Answer is:D
Inside the spherical shell, v is constant
Topper's Solved these Questions
Similar Questions
A point mass m is released from rest at a distance of 3R from the centre of a thin-walled hollow sphere of radius R and mass M as shown. The hollow sphere is fixed in position and the only force on the point mass is the gravitational attraction of the hollow sphere. There is a very small hole in the hollow sphere through which the point mass falls as shown. The velocity of a point mass when it passes through point P at a distance R/2 from the centre of the sphere is
View SolutionA hollow sphere starts pure rolling from rest as shown. The acceleration of centre of mass of sphere is
View Solution
Knowledge Check
A point mass m is released from rest at a distance of 3R from the centre of a thin-walled hollow sphere of radius R and mass M as shown. The hollow sphere is fixed in position and the only force on the point mass is the gravitational attraction of the hollow sphere. There is a very small hole in the hollow sphere through which the point mass falls as shown. The velocity of a point mass when it passes through point P at a distance R/2 from the centre of the sphere is
 A√2GM3RB√5GM3RC√25GM24RDnone of these
A√2GM3RB√5GM3RC√25GM24RDnone of theseA hollow sphere of radius 1m is given a positive charge of 10µC. The electric field at the centre of hollow sphere will be :
A60×103Vm−1B90×103Vm−1CZeroDInfiniteA mass m is placed in the cavity inside hollow sphere of mass M as shown in the figure. The gravitational force on m is
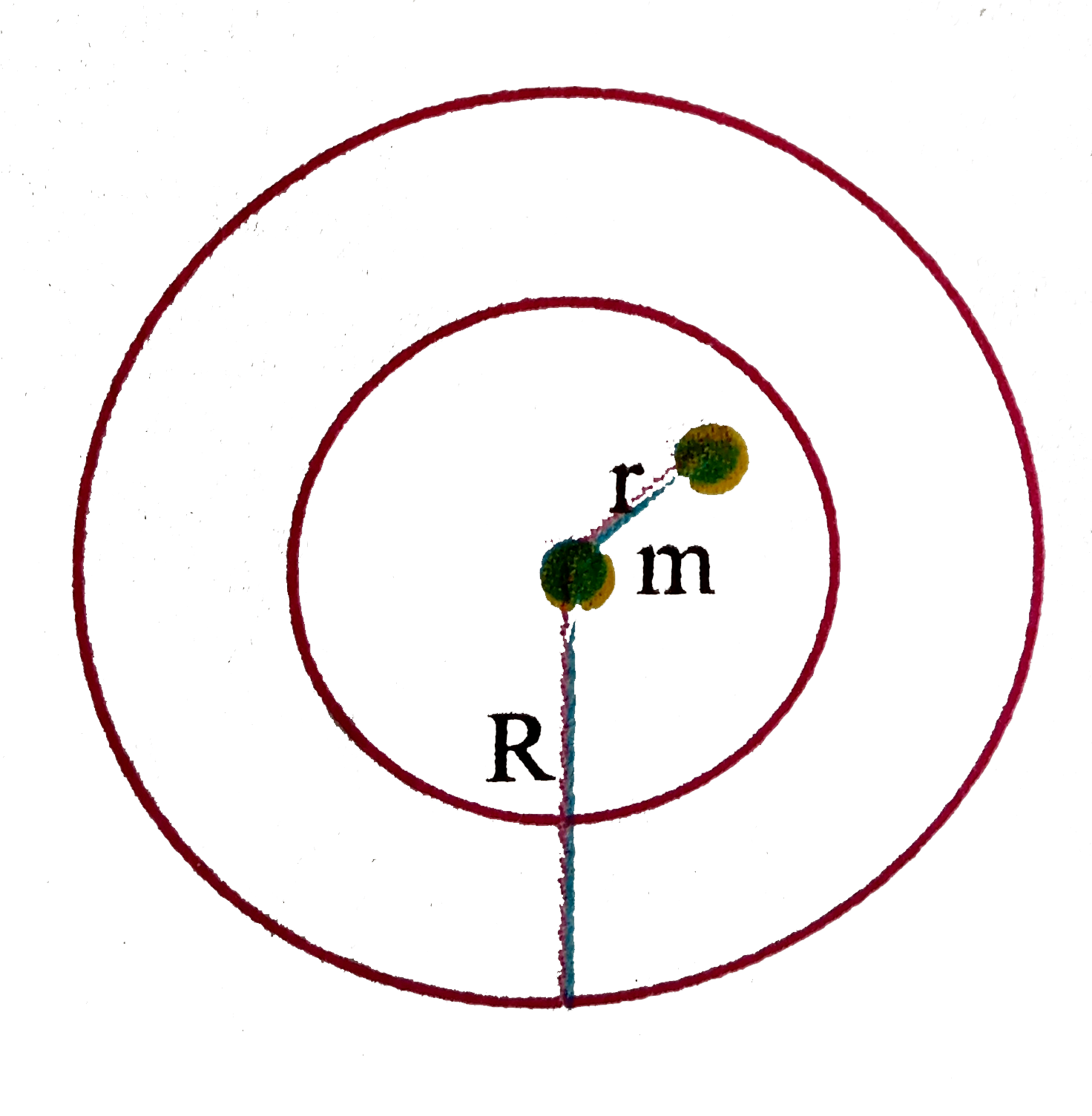 AGMmR2BGMmr2CGMm(R−r)2Dzero
AGMmR2BGMmr2CGMm(R−r)2Dzero
Intensity Of Gravitational Field Due To Hollow Sphere
View SolutionA mass m is placed inside a hollow sphere of mass M as shown in figure. The gravitaional force on mass m is
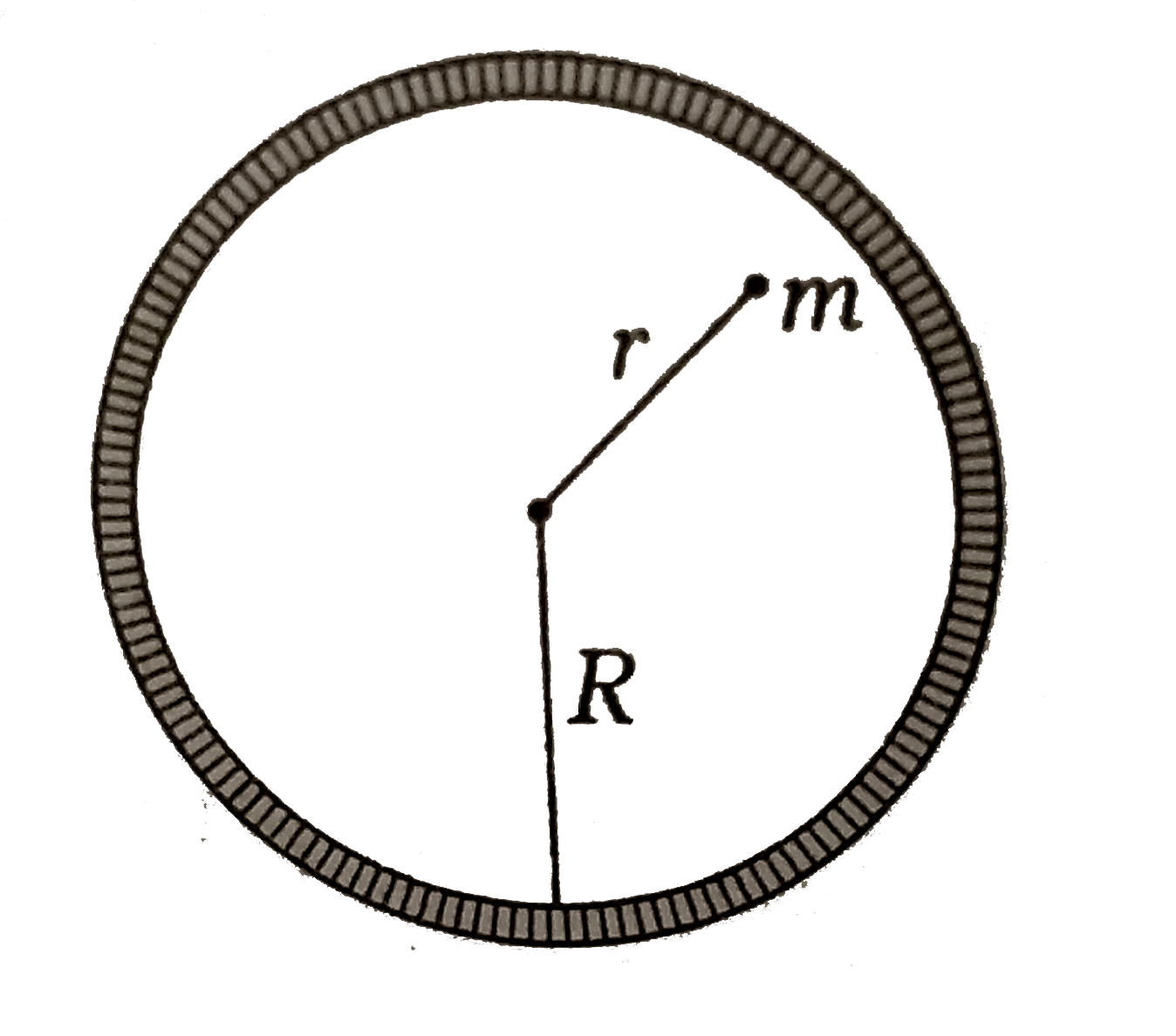
View SolutionA spherical hole is made in a solid sphere of radius R. The mass of the sphere before hollowing was M. The gravitational field at the centre of the hole due to the remaining mass is

View SolutionA mass m is placed inside a hollow sphere of mass M as shown in figure. The gravitaional force on mass m is

View SolutionBy which curve will the variation of gravitational potential of a hollow sphere of radius R with distance be depicted ?
View Solution
