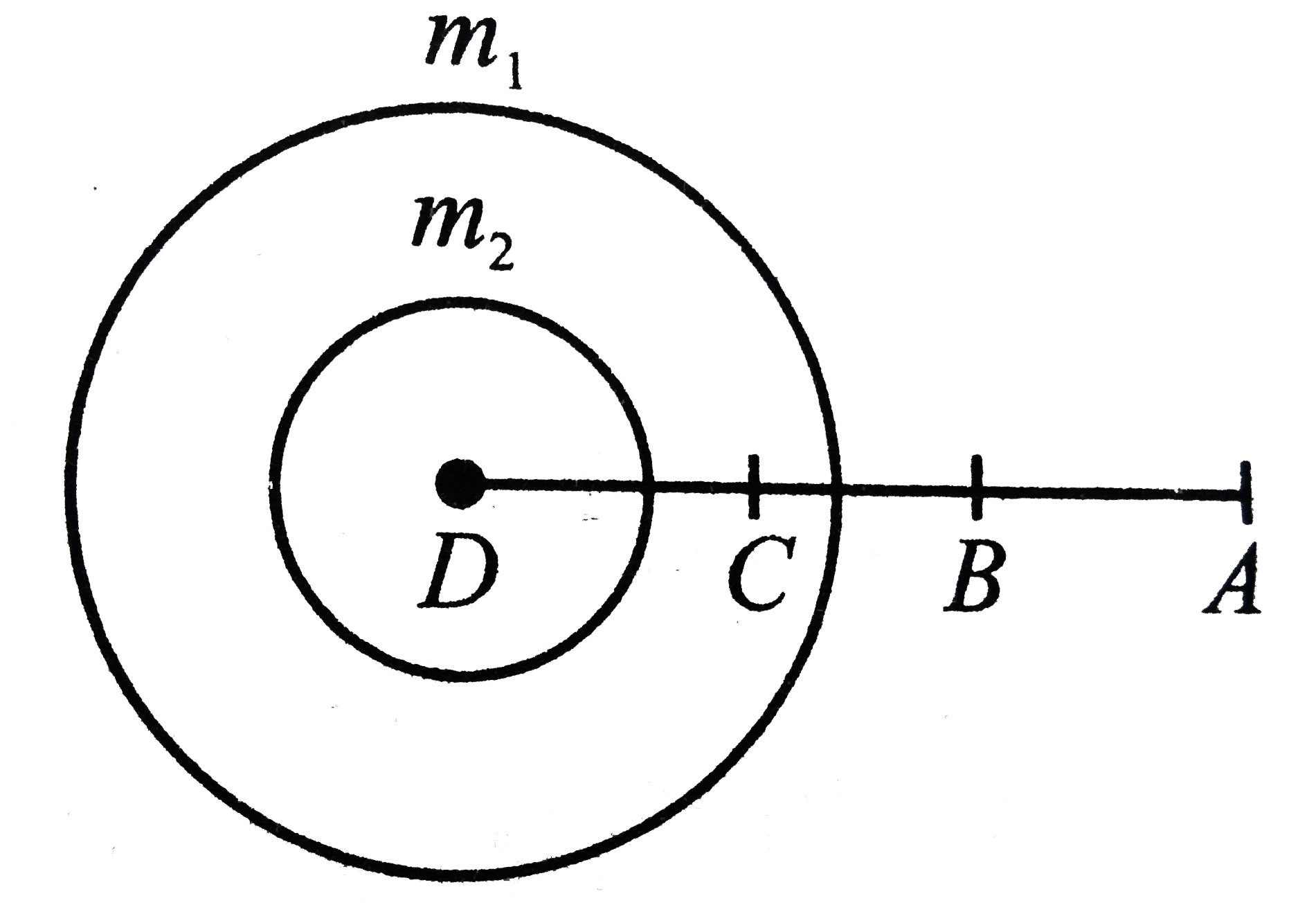
Two concnetric shells of different masses $m_{1}$ and $m_{2}$ are having a sliding particle of mass m. The forces on the particle at position I, II and II are

A

$0, \frac{G m_{1}}{r_{2}^{2}}, \frac{G (m_{1} + m_{2}) m}{r_{1}^{2}}$

B

$\frac{G m_{2}}{r_{2}^{2}}, 0, \frac{G m_{1}}{r_{1}^{2}}$

C

$\frac{G (m_{1} + m_{2}) m}{r_{1}^{2}}, \frac{G m_{2}}{r_{2}^{2}}, 0$

D

$\frac{G (m_{1} + m_{2}) m}{r_{1}^{2}}, \frac{G (m_{2}) m}{r_{2}^{2}}, 0$

Text Solution

Verified by Experts

The correct Answer is:D

Positoni I, $F = \frac{G m (m_{1} + m_{2})}{r_{1}^{2}}$
(here the particle lies outside of both the shells)
Positon II. $F = \frac{G m_{2}}{r_{2}^{2}}$
Here the particle lies outside of the shell of mass $m_{1}$ positon III. Her the particle lies inside of both of th shells of F=0.

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two concentric shells of different mass $m_{1}$ and $m_{2}$ are having a sliding particle of mass $m$ . The forces on the sliding at positions $I, I I$ and $I I I$ are respectively

A $0, \frac{G m_{1}}{r_{2}^{2}}, \frac{G (m_{1} + m_{2}) m}{r_{1}^{2}}$
B $\frac{G m_{2}}{r_{2}^{2}}, 0, \frac{G m_{1}}{r_{1}^{2}}$
C $\frac{G (m_{1} + m_{2}) m}{r_{1}^{2}}, \frac{G m_{2}}{r_{2}^{2}}, 0$
D $\frac{G (m_{1} + m_{2}) m}{r_{1}^{2}}, \frac{G (m_{2}) m}{r_{2}^{2}}, 0$
Question 2 - Select One
The reduce mass of two particles having masses m and 2 m is
A2 m
B3 m
C2 m/3
Dm/2
Question 3 - Select One
The reduce mass of two particles having masses m and 2 m is
A2 m
B3 m
C2 m/3
Dm/2

NARAYNA-GRAVITATION-EXERCISE -IV

Home
Ask Doubt
Profile