A ring having non-uniform distribution of mass M and radius R is being considered. A point mass m0 is taken slowly towards the ring. In doing so, work done by the external force against the gravitational force exerted by ring is

GMm0√2R
GMm0R⎡⎢⎣1√2−1√5
GMm0R[1√5−1√2]
GMm0√5R
The correct Answer is:B
W=m[VB−VA]
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - NCERT BASED QUESTIONS26videos
GRAVITATION
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL -I(H.W)56videos
GRAVITATION
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL II (C.W.)38videos
GRAVITATION
- BOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I6videos
FRICTION
- BOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)52videos
KINETIC THEORY OF GASES
Similar Questions
Find the moment of inertia of uniform ring of mass M and radius R about a diameter.
 View Solution
View SolutionA uniform ring of mass 2m and radius a is placed directly above the uniform sphere of mass M and of same radius. The centre of ring is at distance √3a from the centre of sphere. The gravitational force exerted by the sphere on the ring is NGMma2 units. Calculate is the value of N?
View Solution
Knowledge Check
- Question 1 - Select One
For a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMR - Question 2 - Select One
The total energy of rolling ring of mass m and radius R is
A3/2mv2B1/2mv2Cmv2D5/2mv2 - Question 3 - Select One
A ring of mass m1 and radius R is fixed in space at some location. An external agent brings a point mass m2 from infinity to centre of the ring. Work done by the external agent will be
A−Gm1m2RBGm1m2RCG√m21+m22RDGm1m2R(m21+m22)
A uniform rig of mas m and radius a is placed directly above a uniform sphre of mass M and of equyal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational foerce exerted by the sphere on the ring.
View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity ω. If a increases then tension in ring
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be
 View Solution
View SolutionFind the out the moment of inertia of a ring having uniform mass distribution of mass M and radius R about an axis which is tangent ot the ring and a in the plane of the ring b. perpendicular to the plane of the ring.
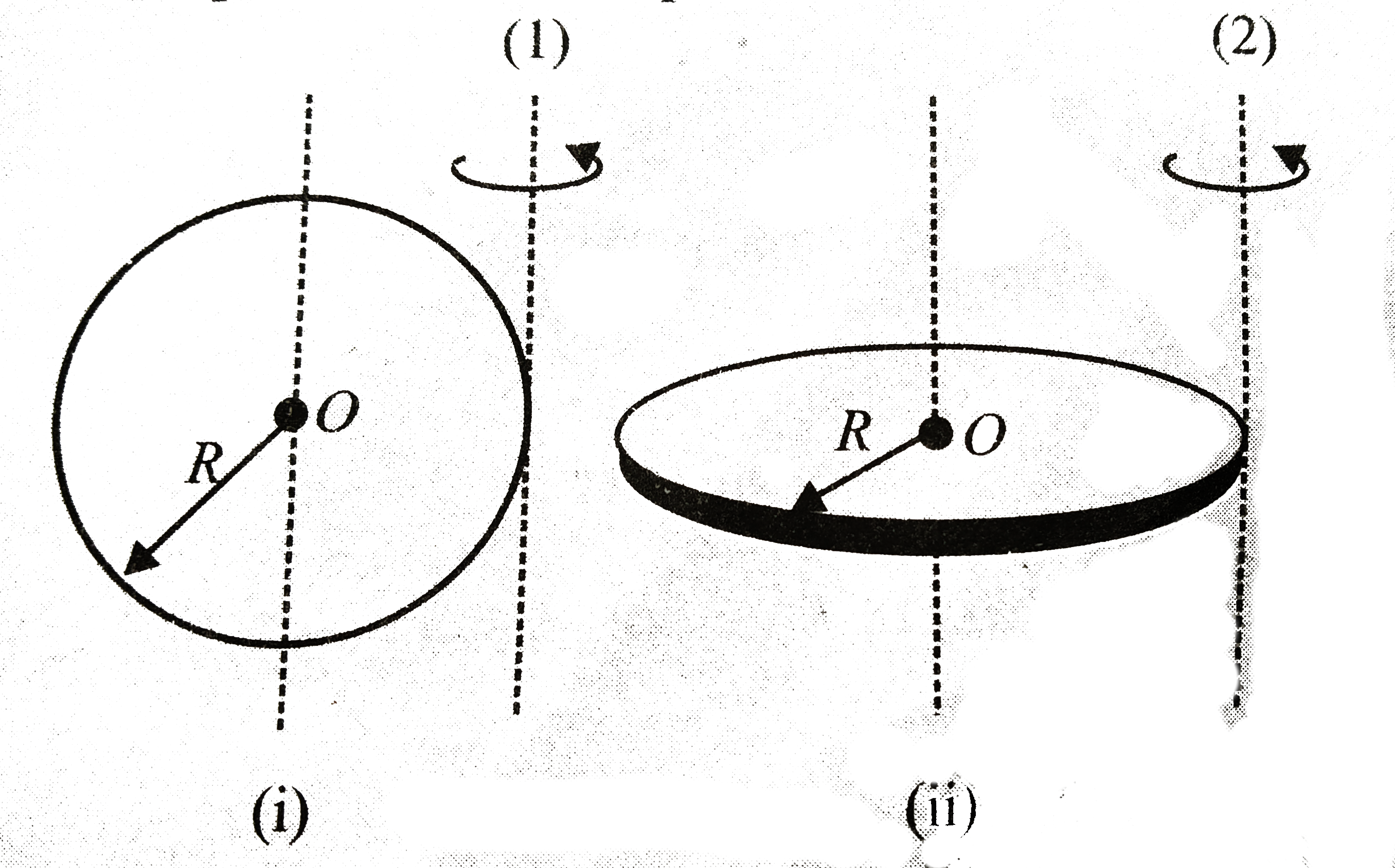 View Solution
View SolutionThe escape velocity form the centre of a unifrom ring of mass M and radius R is :
View Solution

