If g is acceleration due to gravity on the surface of the earth, having radius R, the height at which the acceleration due to gravity reduces to g/2 is
R/2
√2R
R√2
(√2−1)R
The correct Answer is:D
To solve the problem of finding the height at which the acceleration due to gravity reduces to g2, we can follow these steps:
Step 1: Understand the formula for acceleration due to gravity
The acceleration due to gravity g at a distance r from the center of the Earth is given by the formula:
g=GMr2
where G is the universal gravitational constant and M is the mass of the Earth.
Step 2: Set up the equation for gravity at height h
At a height h above the surface of the Earth, the distance from the center of the Earth becomes R+h. The gravitational acceleration at this height is:
g′=GM(R+h)2
Step 3: Set g′ equal to g2
We want to find the height h where the gravitational acceleration is half of that at the surface:
GM(R+h)2=12⋅GMR2
Step 4: Cancel out GM from both sides
Since GM appears on both sides of the equation, we can cancel it out:
1(R+h)2=12R2
Step 5: Cross-multiply to eliminate the fractions
Cross-multiplying gives:
2R2=(R+h)2
Step 6: Expand the right-hand side
Expanding (R+h)2 results in:
2R2=R2+2Rh+h2
Step 7: Rearrange the equation
Rearranging the equation gives:
2R2−R2=2Rh+h2
R2=2Rh+h2
Step 8: Rearranging to form a quadratic equation
This can be rearranged to form a quadratic equation:
h2+2Rh−R2=0
Step 9: Use the quadratic formula to solve for h
Using the quadratic formula h=−b±√b2−4ac2a, where a=1,b=2R,c=−R2:
h=−2R±√(2R)2−4⋅1⋅(−R2)2⋅1
h=−2R±√4R2+4R22
h=−2R±√8R22
h=−2R±2R√22
h=−R+R√2
Step 10: Simplify the expression for height
Thus, the height h can be simplified to:
h=R(√2−1)
Final Answer
The height at which the acceleration due to gravity reduces to g2 is:
h=R(√2−1)
The acceleration due to gravity g at a distance r from the center of the Earth is given by the formula:
g=GMr2
where G is the universal gravitational constant and M is the mass of the Earth.
At a height h above the surface of the Earth, the distance from the center of the Earth becomes R+h. The gravitational acceleration at this height is:
g′=GM(R+h)2
We want to find the height h where the gravitational acceleration is half of that at the surface:
GM(R+h)2=12⋅GMR2
Since GM appears on both sides of the equation, we can cancel it out:
1(R+h)2=12R2
Cross-multiplying gives:
2R2=(R+h)2
Expanding (R+h)2 results in:
2R2=R2+2Rh+h2
Rearranging the equation gives:
2R2−R2=2Rh+h2
R2=2Rh+h2
This can be rearranged to form a quadratic equation:
h2+2Rh−R2=0
Using the quadratic formula h=−b±√b2−4ac2a, where a=1,b=2R,c=−R2:
h=−2R±√(2R)2−4⋅1⋅(−R2)2⋅1
h=−2R±√4R2+4R22
h=−2R±√8R22
h=−2R±2R√22
h=−R+R√2
Thus, the height h can be simplified to:
h=R(√2−1)
The height at which the acceleration due to gravity reduces to g2 is:
h=R(√2−1)
Topper's Solved these Questions
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL-II (H.W)
32 Videos
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL-V
54 Videos
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - NCERT BASED QUESTIONS
26 Videos
- FRICTIONBOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I
6 Videos
- KINETIC THEORY OF GASESBOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)
52 Videos
Similar Questions
Knowledge Check
If g is the acceleration due to gravity on the surface of the earth , its value at a height equal to double the radius of the earth is
AgBg2Cg3Dg9Starting from the centre of the earth having radius R, the variation of g (acceleration due to gravity) is shown by
A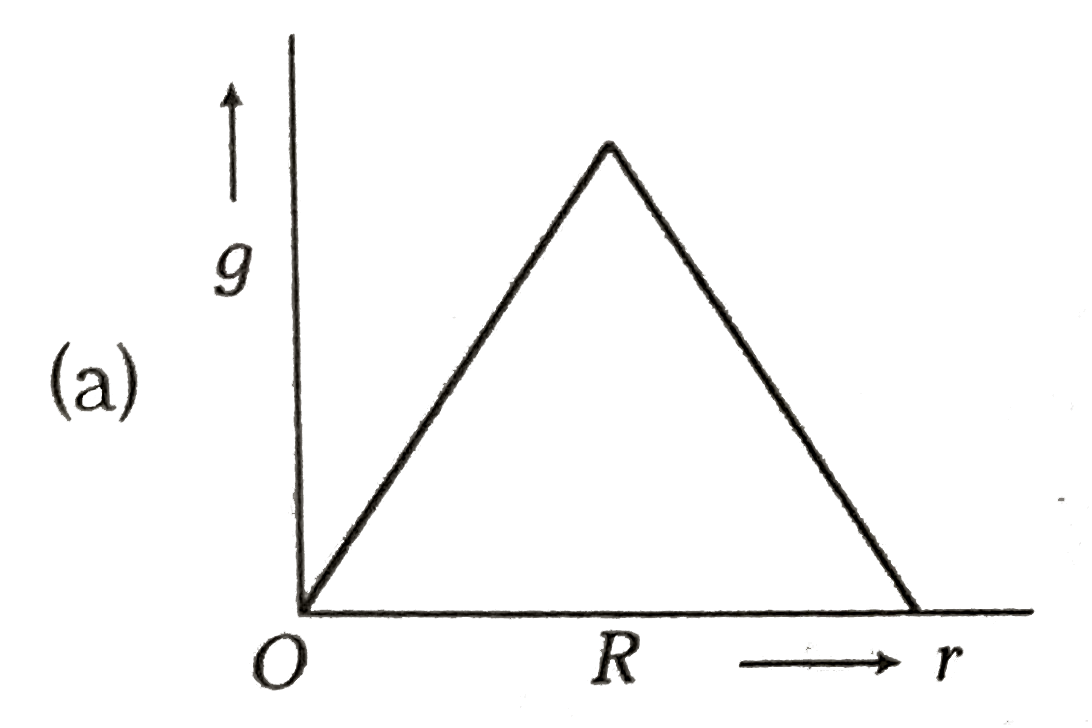 B
B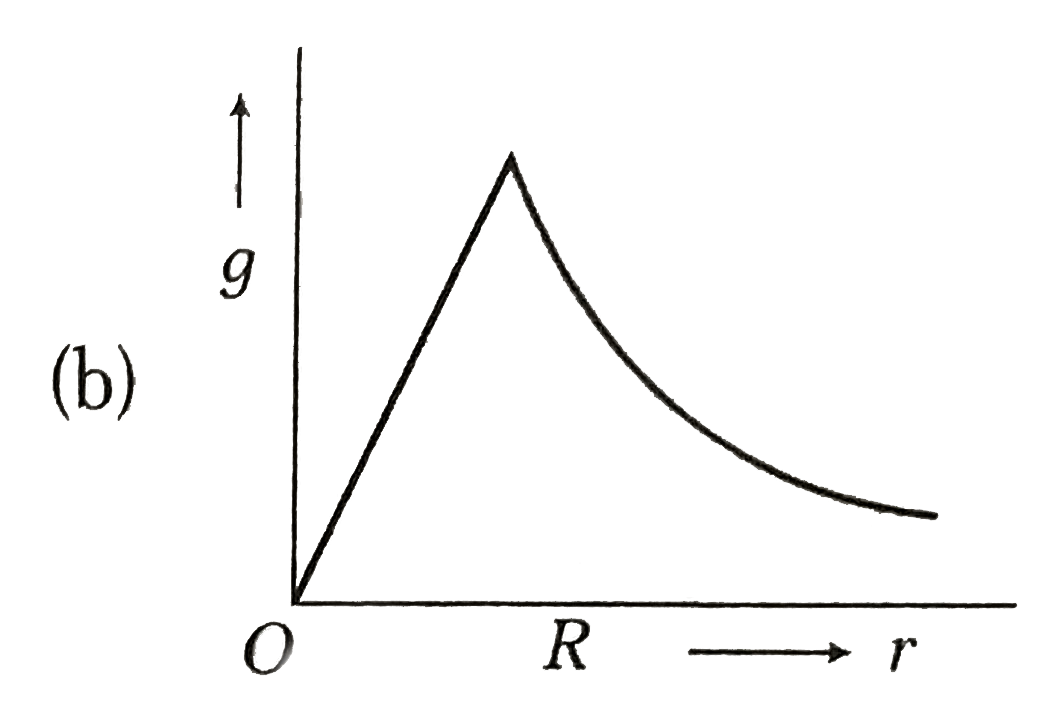 C
C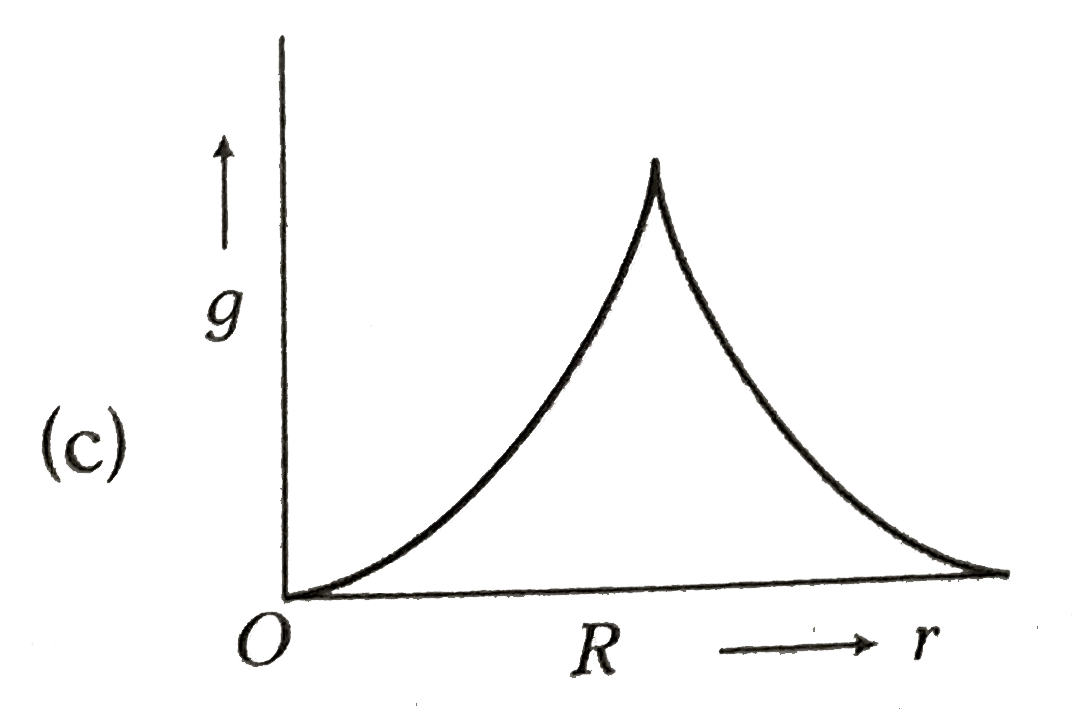 D
D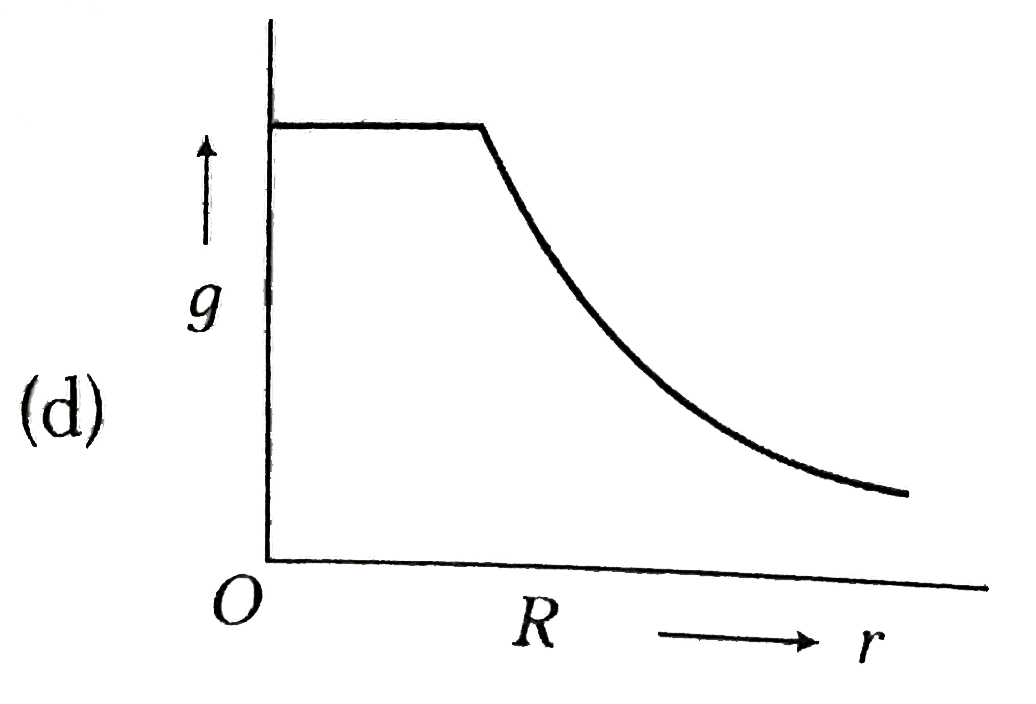
Starting from the centre of the earth having radius R the variation of g (acceleration due to gravity) is shown by
A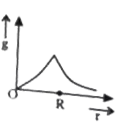 B
B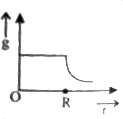 C
C D
D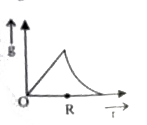
The acceleration due to gravity is _____ at the surface of the earth and ____ at the centre of the earth.
View SolutionIf g is the acceleration due to gravity on the surface of the earth , its value at a height equal to double the radius of the earth is
View SolutionIf the acceleration due to gravity on the surface of earth is g, then the acceleration due to gravity on the surface of a planet whose mass is same as that of earth and radius is twice as that of earth is _________________.
View SolutionIf the acceleration due to gravity on the surface of earth is g, then the acceleration due to gravity on the surface of a planet whose mass is same as that of earth and radius is half as that of earth is _________________.
View SolutionIf g is acceleration due to gravity at the surface of the earth, then its value at a depth of 1/4 of the radius of the earth is
View Solution

