If a spherically symmetric star of radius R collapsed under its own weight, neglecting any forces other than gravitational ones, what is the time required for collapse?
8π2R3(GM)0.5
2π2R3(3GM)0.5
π2R3(8GM)0.5
(2R3GM)0.5
The correct Answer is:A
4πr2dr=volume of an element of thickness dr. The number of particles, ni=4πr2dr.ρ, assumming ρ is the number of the particles per unit volume. The acceleration due to gravity =gR×r for each particle njg=4πr2drρ.gRr=4πgRρr3dr
∴ mean acceleration of the particle due to gravity, g=∫RO(4πRr3dr)ρ(4/3)πR3ρ
Average distance travelled by the particle is =∑nir∑ni⇒¯r=34R
∴¯r=12¯¯¯¯¯at2 where ¯a average acceleration
⇒34R=12.3/4g.t2⇒t=√2Rg
g=GMR2⇒(2R.R2GM)1/2=(2R3GM)0.5
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL-VI42videos
GRAVITATION
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - ILLUSTRATION49videos
GRAVITATION
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL-II (H.W)32videos
GRAVITATION
- BOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I6videos
FRICTION
- BOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)52videos
KINETIC THEORY OF GASES
Similar Questions
A large non rotating star of mass M and radius R begins to collapse under its own gravity and ultimately becomes very small (nearly a point mass). Assume that the density remains uniform inside the sphere in any stage. Plot the variation of gravitational field intensity (well, you can call it cceleration due to gravity) at a distance R2from the centre vs the radius (r) of the star.
View SolutionMass M, of a planet earth is uniformly distributed over a spherical volume of radius R. Calculate the energy needed to deassemble the planet against the gravitational pull ammongst its consituent particles. Given
mR=2.5×1031kgm and g=10ks−2.View Solution
Knowledge Check
- Question 1 - Select One
A dielectric sphere of radius 10 cm has a charge of 3 mC distributed uniformly throughout its volume. The dielectric constant of the material of the sphere is 1. A bullet having charge 3 mc and mass 10 g is fired from the surface of the sphere along the diameter, directly towards its centre. Assuming the sphere to be fixed and neglecting any forces other than electrostatic force, the minimum velocity of the bulge so that it can emerge from the other side of the sphere is
A3×103ms−1B3×106ms−1C9×106ms−1D9×103ms−1 - Question 2 - Select One
Supernova refer to the explosion of a massive star. The material in the central case of such a star continues to collapse under its own gravitational pull. If mass of the core is less is than 1.4 times the mass of sun, its collapse finally results in a white dwarf star. However, if the core has a mass greater than this, it could end up soon as a neutron. star and if its mass is more than about three solar masses, the collapse may still continue till the star becomes a very small object with an extremely high value of density called a 'Black hole'. Escape speed for a black hole is very large. The figure shows a block hole of radius R and another concentric sphere of radius RS, called the 'Schwarzschild Radius'. It is the critical radius at which escape speed equals the speed of light c. Nothing even the light, can escape from within the sphere of Radius RS. So light from a black hole can not escape and hence the terminology 'black hole'. There has been astronomical evidence of a small and massive object at the centre of our galaxy the 'Milky way'. Suppose that there is a particle at a distance about 6 light years. that orbits this massive object with an orbital speed of about 2×105m/s. Use the given data whereever necessary and answer the questions that hollow. G=6.67×10−11N−m2/kg2, Solar mass M=2×1030kg,C=3×108m/s,1 light year =9.5×1015m.
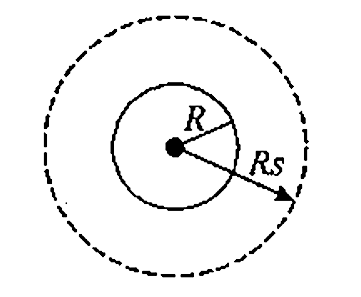
If mass of earth ME≈6×1024kg and its radius RE=6400km, to what fraction of its presents radius does the earth need to be compressed in order to become a black hole ?
(Give only the order of your answer)A10−4B10−9C10−7D10−14 - Question 3 - Select One
Supernova refer to the explosion of a massive star. The material in the central case of such a star continues to collapse under its own gravitational pull. If mass of the core is less is than 1.4 times the mass of sun, its collapse finally results in a white dwarf star. However, if the core has a mass greater than this, it could end up soon as a neutron. star and if its mass is more than about three solar masses, the collapse may still continue till the star becomes a very small object with an extremely high value of density called a 'Black hole'. Escape speed for a black hole is very large. The figure shows a block hole of radius R and another concentric sphere of radius RS, called the 'Schwarzschild Radius'. It is the critical radius at which escape speed equals the speed of light c. Nothing even the light, can escape from within the sphere of Radius RS. So light from a black hole can not escape and hence the terminology 'black hole'. There has been astronomical evidence of a small and massive object at the centre of our galaxy the 'Milky way'. Suppose that there is a particle at a distance about 6 light years. that orbits this massive object with an orbital speed of about 2×105m/s. Use the given data whereever necessary and answer the questions that hollow. G=6.67×10−11N−m2/kg2, Solar mass M=2×1030kg,C=3×108m/s,1 light year =9.5×1015m.
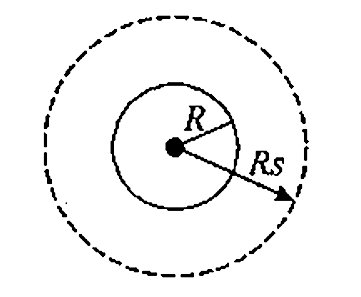
Theories suggest that it is not possible for a single star to have a mass of more than 50 masses. The massive object at the centre of milky way galaxy is most likely to be a :Awhite dwarfBneutron starCblack holeDsingle ordinary star
Supernova refer to the explosion of a massive star. The material in the central case of such a star continues to collapse under its own gravitational pull. If mass of the core is less is than 1.4 times the mass of sun, its collapse finally results in a white dwarf star. However, if the core has a mass greater than this, it could end up soon as a neutron. star and if its mass is more than about three solar masses, the collapse may still continue till the star becomes a very small object with an extremely high value of density called a 'Black hole'. Escape speed for a black hole is very large. The figure shows a block hole of radius R and another concentric sphere of radius RS, called the 'Schwarzschild Radius'. It is the critical radius at which escape speed equals the speed of light c. Nothing even the light, can escape from within the sphere of Radius RS. So light from a black hole can not escape and hence the terminology 'black hole'. There has been astronomical evidence of a small and massive object at the centre of our galaxy the 'Milky way'. Suppose that there is a particle at a distance about 6 light years. that orbits this massive object with an orbital speed of about 2×105m/s. Use the given data whereever necessary and answer the questions that hollow. G=6.67×10−11N−m2/kg2, Solar mass M=2×1030kg,C=3×108m/s,1 light year =9.5×1015m.
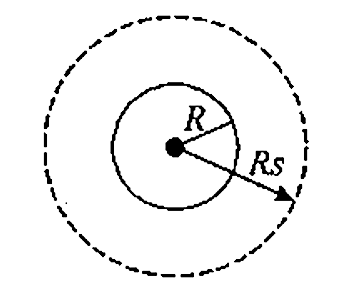
Mass (in kg) of the massive object at the centre of the milky galaxy is of the order :View SolutionTwo stars bound together by gravity orbit othe because of their mutual attraction. Such a pair of stars is referred to as a binary star system. One type of binary system is that of a black hole and a companion star. The black hole is a star that has cullapsed on itself and is so missive that not even light rays can escape its gravitational pull therefore when describing the relative motion of a black hole and companion star, the motion of the black hole can be assumed negligible compared to that of the companion.
The orbit of the companion star is either elliptical with the black hole at one of the foci or circular with the black hole at the centre. The gravitational potential energy is given by U=−GmM/r where G is the universal gravitational constant, m is the mass of the companion star, M is the mass of the black hole, and r is the distance between the centre of the companion star and the centre of the black hole. Since the gravitational force is conservative. The companion star and the centre of the black hole, since the gravitational force is conservative the companion star's total mechanical energy is a constant. Because of the periodic nature of of orbit there is a simple relation between the average kinetic energy <K> of the companion star Two special points along the orbit are single out by astronomers. Parigee isthe point at which the companion star is closest to the black hole, and apogee is the point at which is the farthest from the black hole.
Q. For circular orbits the potential energy of the companion star is constant throughout the orbit. if the radius of the orbit doubles, what is the new value of the velocity of the companion star?View SolutionTwo spherical soap bubbles of radii r1 and r2 in vacuume collapse under isothermal condition. The resulting bubble has radius R such that
View SolutionConsider two solid uniform spherical objects of the same density ρ. One has radius R and the other has radius 2R. They are in outer space where the gravitational fields from other objects are negligible. If they are arranged with their surface touching, what is the contact force between the objects due to their traditional attraction?
View SolutionTwo point masses M are kept fixed on the x-axis at a distance a from the origin, another point mass m is moving in a circular path of radius R (in y - z plane) under the influence of gravitational force of attraction, then speed of m will be (Assume no forces are acting on m other than the gravitational forces by two M)
 View Solution
View Solution

