A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. A particle is released from one end of the tunnel. The pressing force by the particle on the wall, and the acceleration of the particle vary with x (distance of the particle from the centre) according to
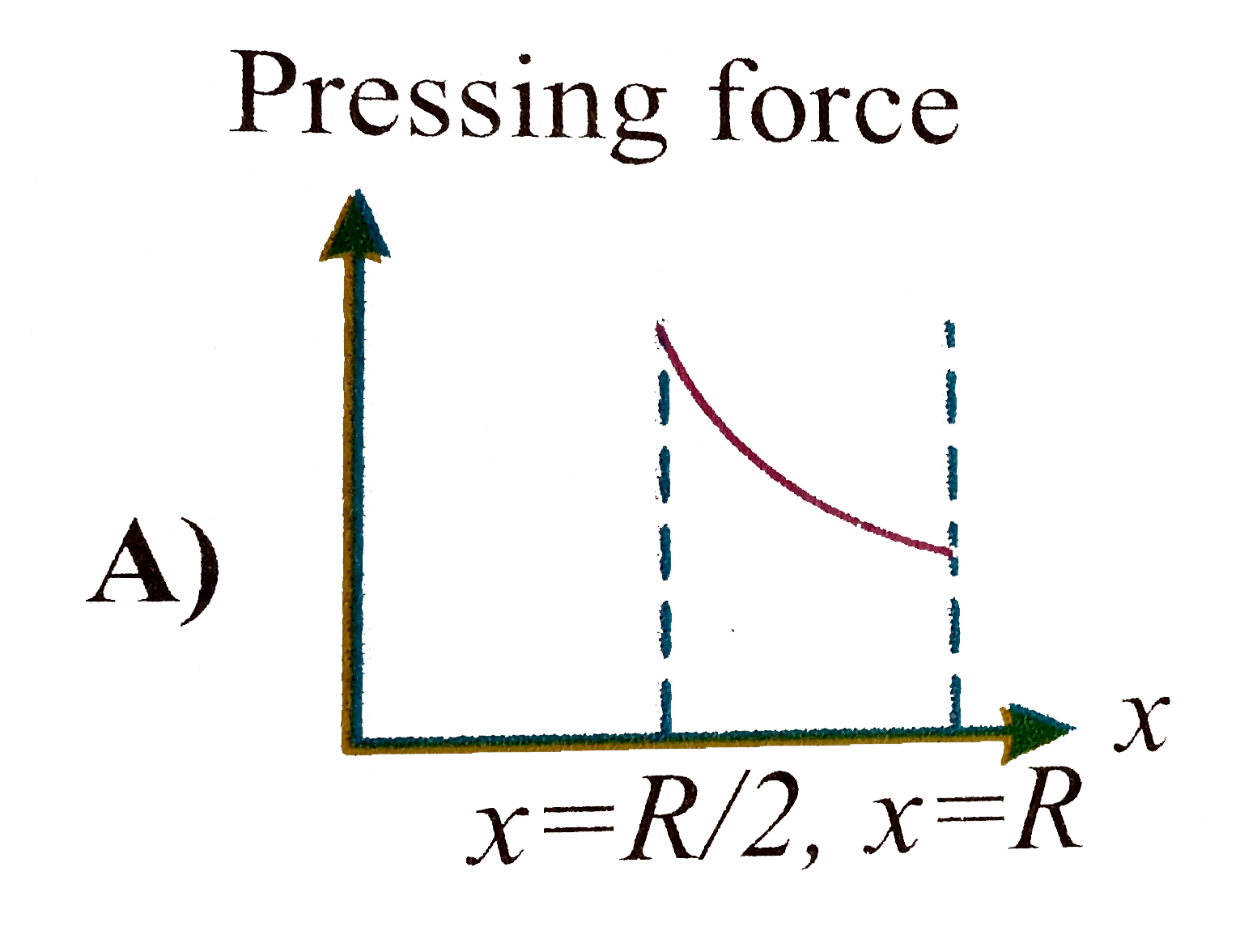
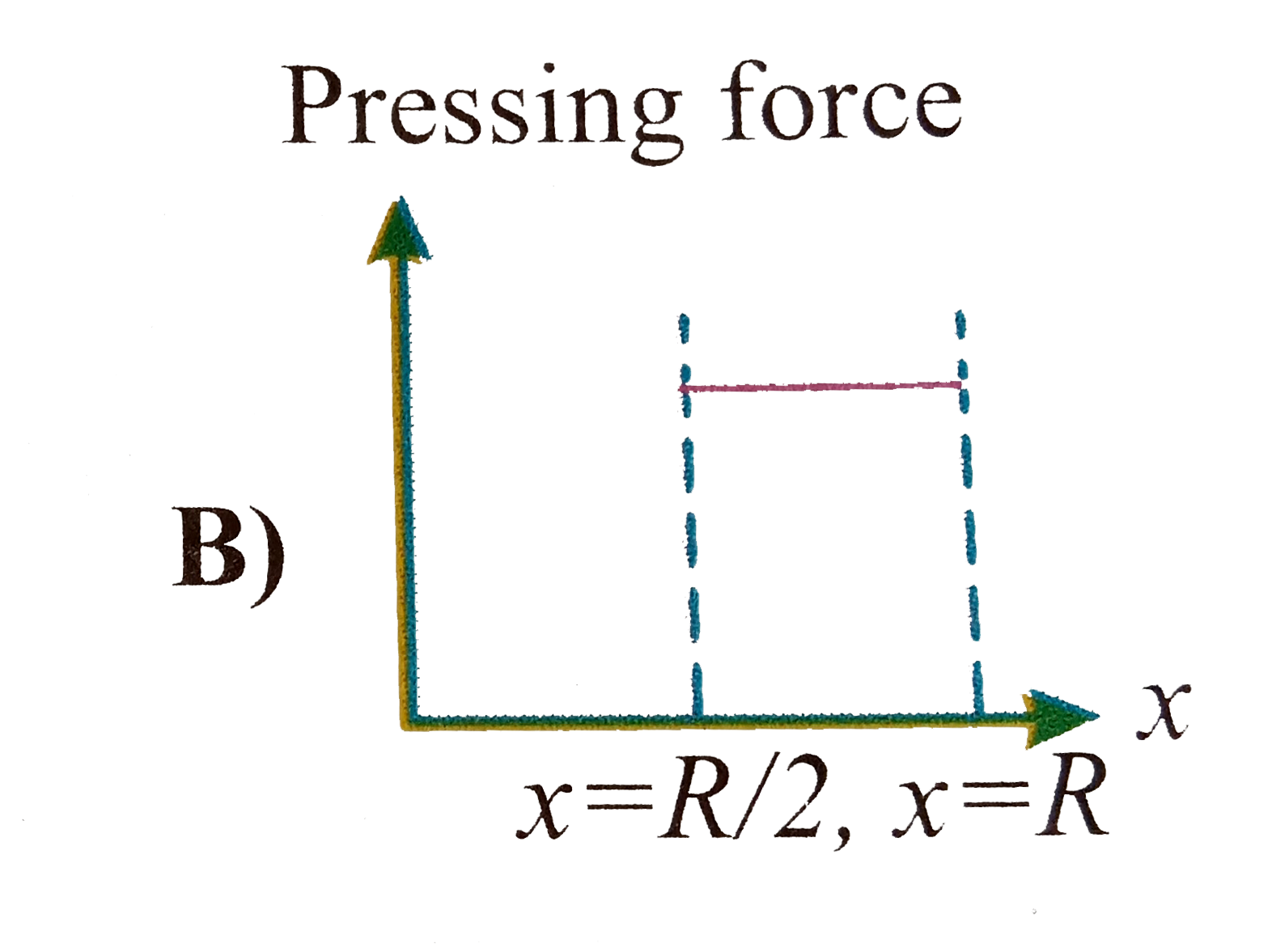
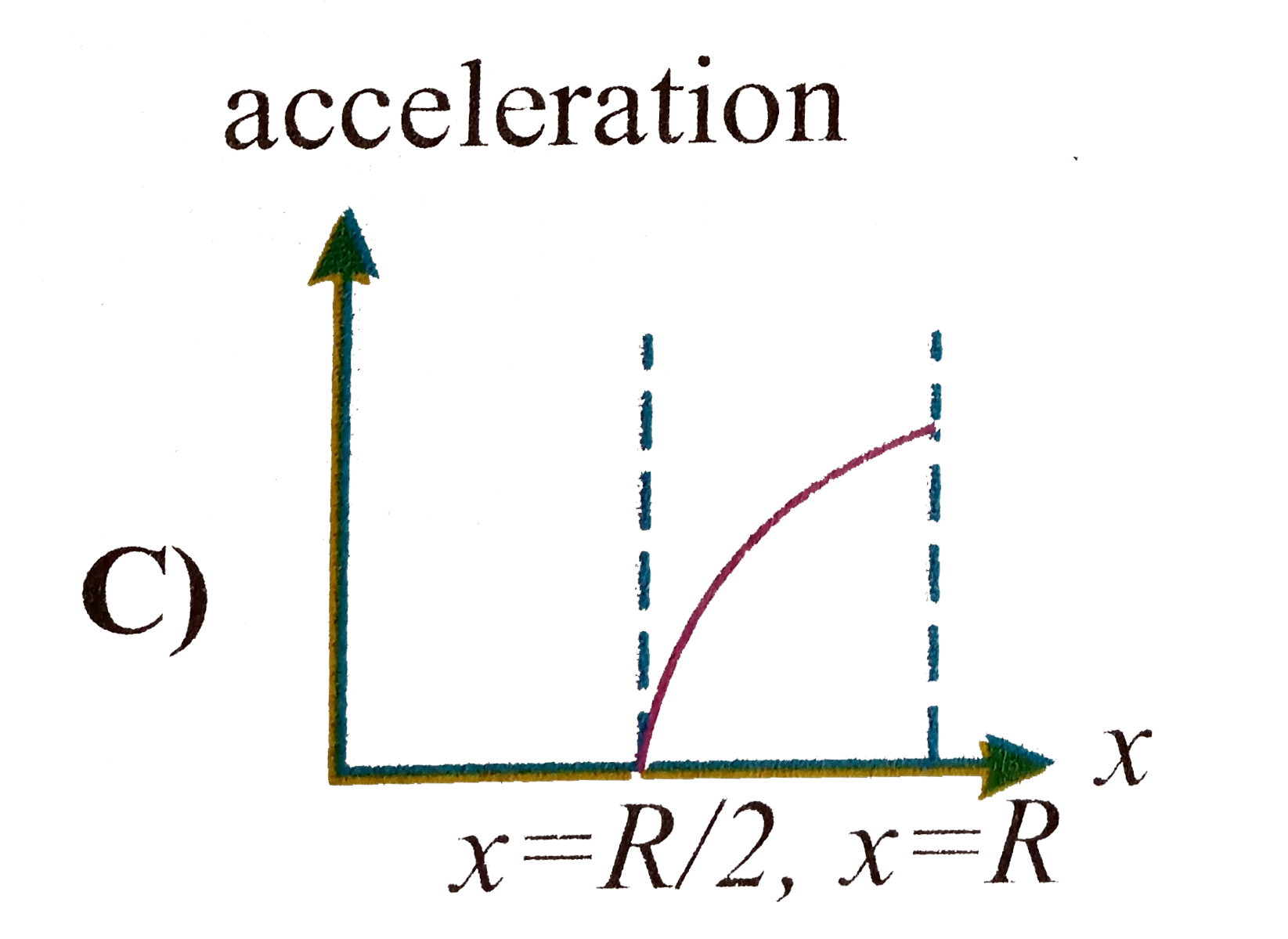
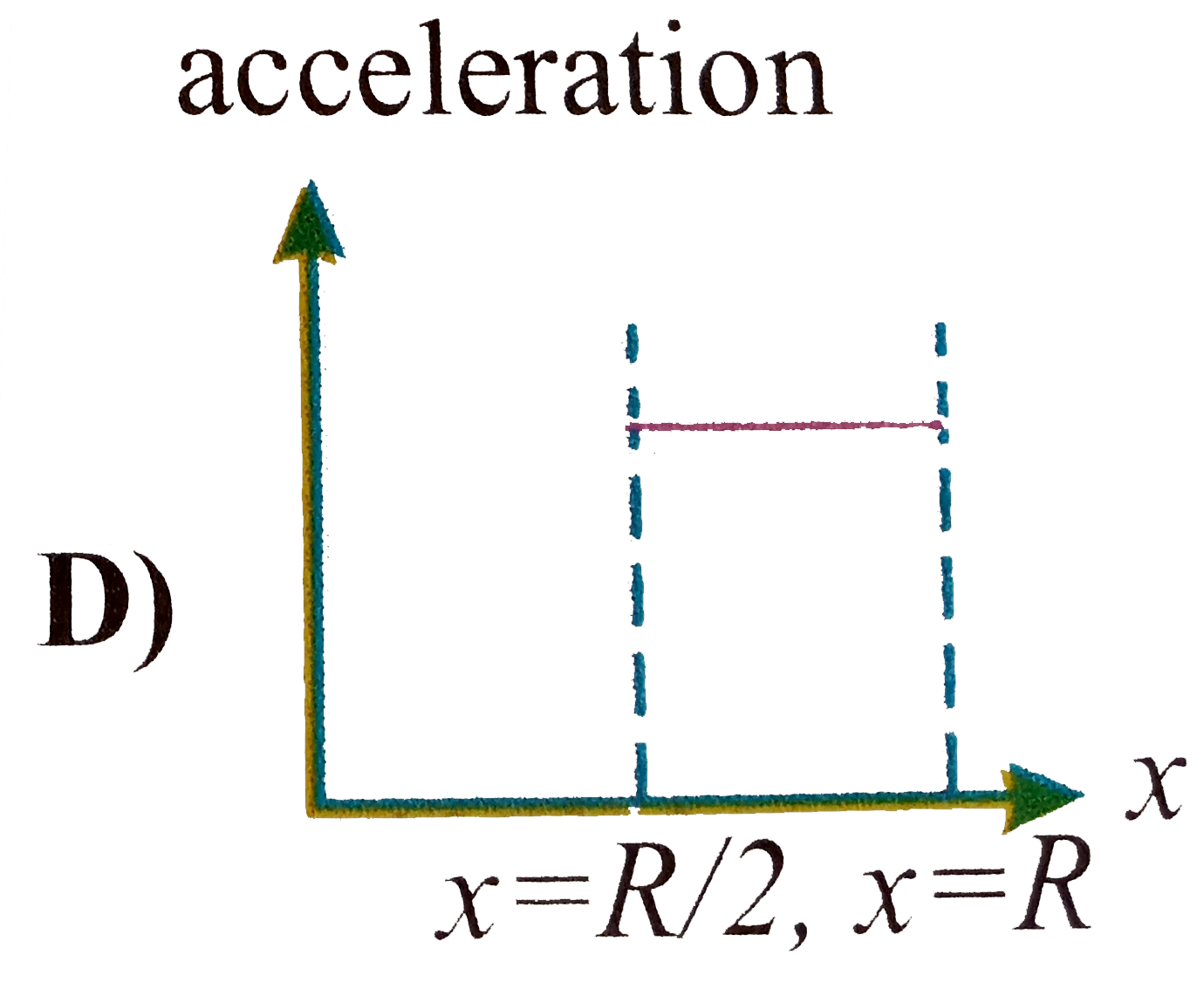
The correct Answer is:B, C
Net force towards centre of earth =mg'=(mgx)/R,
Normal force N=mg'sinθ
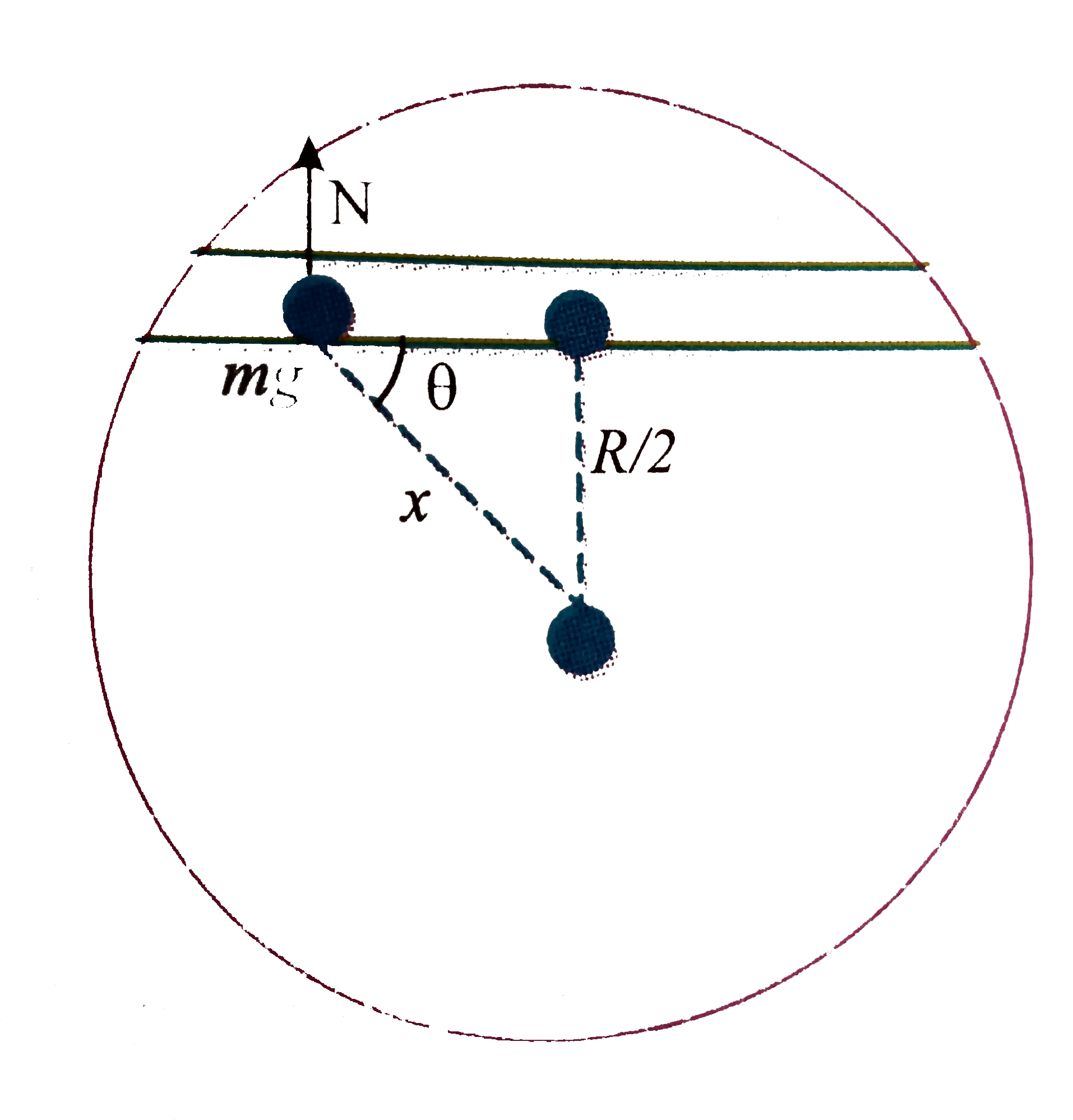
Thsu pressing force N=mgxRR2x
N=mg2 is constant and independent of x.
Hence (b). Tangential force F=ma=mg'cosθ
Q=g'cosθ=gxR√x2−R22x
a=gxR√R2−4x2.
Curve is parabolic and at x=R2,a=0. hence (C)
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL-VI42videos
GRAVITATION
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - ILLUSTRATION49videos
GRAVITATION
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL-II (H.W)32videos
GRAVITATION
- BOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I6videos
FRICTION
- BOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)52videos
KINETIC THEORY OF GASES
Similar Questions
A tunnel ois dug along a chord of the earth a perpendicular distance R2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the eall on a particle of mass m when it is at a distance x from the centre of the tunnel.
View SolutionAssume that a tunnel is dug along a cord of earth at a perpendicular distance R2 from earth's centre where R is the radius of earth. The wall of tunnel is frictionless. Find the time period of particle excuting SHM in tunnel
View Solution
Knowledge Check
- Question 1 - Select One
Assume that a tunnel is dug along a chord of the earth, at a perpendicular distance (R/2) from the earth's centre, where 'R' is the radius of the Earth. The wall of the tunnel is frictionless. If a particle is released in this tunnel, it will execute a simple harmonic motion with a time period :
A2πRgBg2πrC12π√grD2π√Rg - Question 2 - Select One
A tunnel is dug across the earth of mass 'M' and radius 'R' at a distance R/2 from the centre 'O' of the Earth as shown. A body is released from rest from one end of the smooth tunnel. The velocity acquired by the body when it reaches the centre 'C' of the tunnel is
 A√3GM2RB√3GM4RC√3GM8RDd√3GM16R
A√3GM2RB√3GM4RC√3GM8RDd√3GM16R - Question 3 - Select One
If a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Maximum speed of the particle isA√2GMRB√GMRC√3GM2RD√GM2R
(a) A tunnel is dug along a diameter of the earth. Find the force on the a particle of mass m placed in the tunnel at a distance x from the centre.
(b) A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. the wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.View SolutionAssume that a tunnel is dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless.
(a) Find the gravitational force exerted by the earth on a particle of mass m placed in the tunnel at a distance x from the centre of the tunnel.
(b) Find the component of this force along the tunnel and perpendicular to the tunnel.
(c) Find the normal force exerted by the wall on the particle.
(d) Find the resultant force on the particles.
(e) Show that the motion of the particle in the tunnel is simple harmonic and find the time period.View SolutionAssume that a tunnel ils dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless. a. Find the gravitational force exerted by the earth on a particle of mass m placed in the tunnel at a distance x from the centre of the tunnel. b. Find the component of this fore along the tunnel and perpendicular to the tunnel. c. Find the normal force exerted by the wall on the particle. d. Find the resultant force on the particle. e.Show that the motion of the particle in the tunnel is simple harmonic and find the time period.
View SolutionSuppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point a distance h directly above the tunnel. The motion of the particle as seen from the earth is
View SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Time period of the particle is not equal toView Solution

