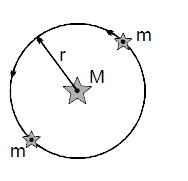
![A triple star system consists of two stars each of mass m in the same circular orbit about central star with mass M=2xx10^(33)kg. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=10^(11) m and the orbital period each star is 1.6xx10^(7)s [take pi^(2)=10 and G=(20)/(3)xx10^(-11)Mn^(2)kg^(-2)] Q. The mass m of the outer stars is:](https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_C08(II)_S01_033_Q01.png)
A triple star system consists of two stars each of mass m in the same circular orbit about central star with mass M=2×1033kg. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=1011 m and the orbital period each star is 1.6×107s [take π2=10 and G=203×10−11Mn2kg−2]
Q. The mass m of the outer stars is:
1615×1030kg
118×1030kg
1516×1030kg
811×1030kg
The correct Answer is:B
Fmm=Gravitational force between two outer stars =Gm24r.
FmM=Gravitational force between central star and outer star=GmMr2 for circular motion of outer star, mv2r=Fmm+FmM
∴V2=G(m+4M)4r
T=period of orbtal motion =2πrv
m=16π2r2GT2−4M=(15016−8)1030=118×1030kg
Topper's Solved these Questions
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL-VI
42 Videos
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - ILLUSTRATION
49 Videos
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL-II (H.W)
32 Videos
- FRICTIONBOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I
6 Videos
- KINETIC THEORY OF GASESBOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)
52 Videos
Similar Questions
A certain triple-star system consists of two stars, each of mass m, revolving about a central star, mass M, in the same circular orbit. The two stars stay at opposite ends of a diameter of the circular orbit, see figure. Derive an expression for the period of revolution of the stars, the radius of the orbit is r.
View SolutionThe radius of the nearly circular orbit of mercury is 5.8×1010 m and its orbital period is 88 days. If a hypothetical planet has an orbital period of 55 days, what is the radius of its circular orbit ?
View Solution
Knowledge Check
_S01_034_Q01.png)
A triple star ststem consists of two stars each of mass m in the same circular orbit about central star with mass M=2×1033kg. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=1011 m and the orbital period each star is 1.6×107s [take π2=10 and G=203×10−11Mn2kg−2]
Q. The orbital velocity of each star isA54√10×10/sB54√10×105m/sC54√10×102m/sD54√10×104m/s_S01_035_Q01.png)
A triple star ststem consists of two stars each of mass m in the same circular orbit about central star with mass M=2×1033kg. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=1011 m and the orbital period each star is 1.6×107s [take π2=10 and G=203×10−11Mn2kg−2]
Q. The total machanical energy of the system isA−137564×1035JB−137564×1038JC−137564×1034JD−137564×1037J_S01_033_Q01.png)
A triple star system consists of two stars each of mass m in the same circular orbit about central star with mass M=2×1033kg. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=1011 m and the orbital period each star is 1.6×107s [take π2=10 and G=203×10−11Mn2kg−2]
Q. The mass m of the outer stars is:A118×1030B1516×1030C403×1030D203×1030
Orbit of a planet around a star is
View SolutionOrbit of a planet around a star is
View SolutionAn isolated triple star systerm consists of two identical stars, each of mass m and f fixed star of mass M. They revolve around the central star in the same circular orbit to radius r. The orbiting stars are always at opposite ends of a diameter of the orbit. The time period of revolution of each star around the fixed is equal to:

View SolutionA system consists of two stars of equal masses that revolve in a circular orbit about their centre of mass . Orbital speed of each star is v and period is T . Find the mass M of each star . (G is gravitational constant )
View SolutionA binary star system consists of two stars. One star has twice the mass of the other. The star rotates about their common centre of mass. Which of the following statement is correct?
View Solution
