In astronomy order of magnitude estimation plays an important role. The derivative dpdt can be taken difference ration ΔPΔr. Consider the star has a radius R, pressure at its centre is Pe and pressure at outer layer is zero is the average mass is MQ2 and average radius Ro2 then the expression for Pc is
Pc=32GM20πR40
Pc=23πGM20R40
Pc=23GM20πR40
Pc=32GM20R40
The correct Answer is:A
The net force acting on the system is
∣∣→F1+→F2∣∣=0
⇒ the linear momentum of the system is conserved
⇒mAvA=mBvB
⇒vA=mBmAvB=21×3.6=7.2cm/hr
=7.2×10−23.6×103=7.2×10−23600=7.2×10−23.6×103=2×10−5
In 10−5m/s,vA=2
Topper's Solved these Questions
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - ILLUSTRATION
49 Videos
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - EVALUATE YOURSELF -1
3 Videos
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL-V
54 Videos
- FRICTIONBOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I
6 Videos
- KINETIC THEORY OF GASESBOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)
52 Videos
Similar Questions
A star can be considered as a shpherical ball of hot gas of radius R.Inside the star the density of the gas is ρr at a radius r and mass of the gas within this region is Mr.The correct differential equation for variation of mass with respect to radius (dMrdt) is (refer to the adjacent figure)

In astronomy order of magnitude estimation plays an important role. The derivative dpdr can be taken difference ratio ΔPΔr . Consider the star has a radius R, pressure at its centre is PC and pressure at outer layer is zero if the average mass is M02 and average radius R02 then the expression for PC is
View SolutionA uniform sphere has a mass M and radius R. Find the pressure p inside the sphere, caused by gravitational compression, as a function of the distance r from its centre. Evaluate p at the centre of the Earth, assuming it to be a uniform sphere.
View Solution
Knowledge Check
A star can be considered as spherical ball of hot gas of radius R. Inside the star, the density of the gas is ρr at radius r and mass of the gas within this region is Mr.
A star in it's prime age is said to be under quilibrium due to gravitational pull and outward radiation pressure (p). consider the shell of thikness dr as in the figure of previous question. if the pressure on this shell is dp then the correc equation is (G is universal gravitational constant)Adpdr=−GMrr2ρrBdpdr=GMrr2ρrCdpdr=−23GMrr2ρrDdpdr=23GMrr2ρrA point P lies on the axis of a fixed ring of mass M and radius R, at a distance 2R from its centre O. A small particle starts from P and reaches O under gravitational attraction only. Its speed at O will be
A ⎷2GMR(1−1√5)B√2GMRC√2GMR(√5−1)DzeroConsider a hypothetical solar system, which has two identical massive suns each of mass M and radius r, seperated by a seperation of 2√3R (centre to centre). (R gtgtgtr). These suns are always at rest. There is only one planet in this solar system having mass m. This planet is revolving in circular orbit of radius R such that centre of the orbit lies at the mid point of the line joining the centres of the sun and plane of the orbit is perpendicular to the line joining the centres of the sun. Whole situation is shown in the figure.

Q. Average force on the planet in half revolution isAGMm4πR2BGMm4R2CGMm2πR2DGMm8R2
A uniform sphere has a mass M and radius R. Find the pressure p inside the sphere, caused by gravitational compression, as a function of the distance r from its centre. Evaluate p at the centre of the Earth, assuming it to be a uniform sphere.
View SolutionAn infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R2 with its center on the axis of the cylinder, as shown in the figure. The magnitude of the electric field at the point P, which at a distance 2 R (from the axis of the cylinder, is given by the expression 23ρR16nɛ0, The value of n is
'(##CEN_KSR_PHY_JEE_C18_E01_040_Q24##)'
View SolutionA star can be considered as a shpherical ball of hot gas of radius R.Inside the star the density of the gas is ρr at a radius r and mass of the gas within this region is Mr.The correct differential equation for variation of mass with respect to radius (dMrdt) is (refer to the adjacent figure)

Assuming that the gas inside the sun behaves very much like the perfect gas, the temperature at the centre of the sun is nearly (the number density of gas particles =2ρMH , Boltzmann constant KB=1.4×10−23J.K−1 and mass of proton MH=1.67×10−27kg)
View SolutionAn infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R/2 with its centre on the axis of cylinder, as shown in the figure. The magnitude of the electic field at the point P, which is at a distance 2R form the axis of the cylinder, is given by the expression 23rR16ke0 . The value of k is .
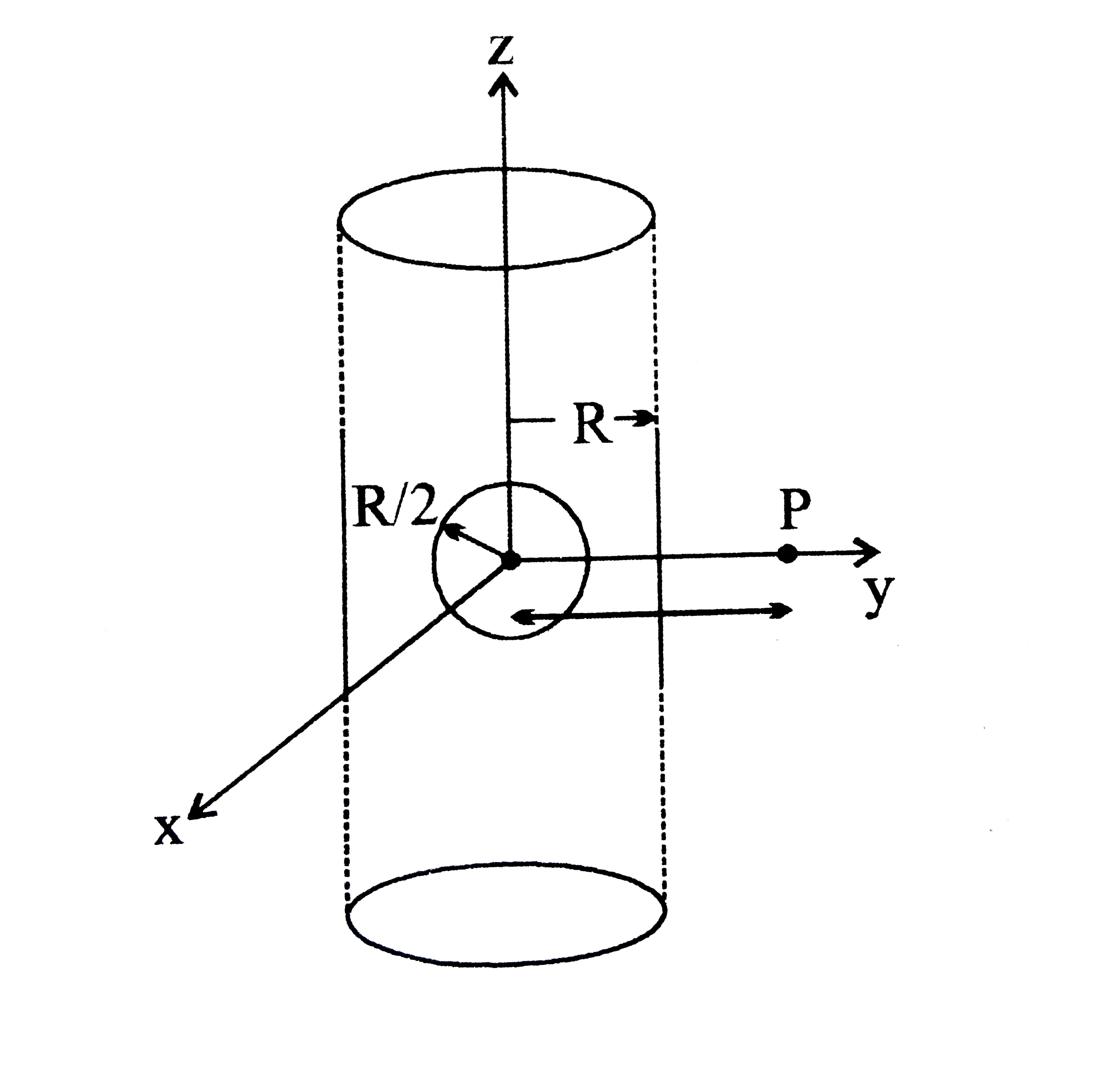 .
.
View SolutionAn infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R/2 with its centre on the axis of cylinder, as shown in the figure. The magnitude of the electric field at the point P, which is at a distance 2R form the axis of the cylinder, is given by the expression 23rR16ke0 . The value of k is .
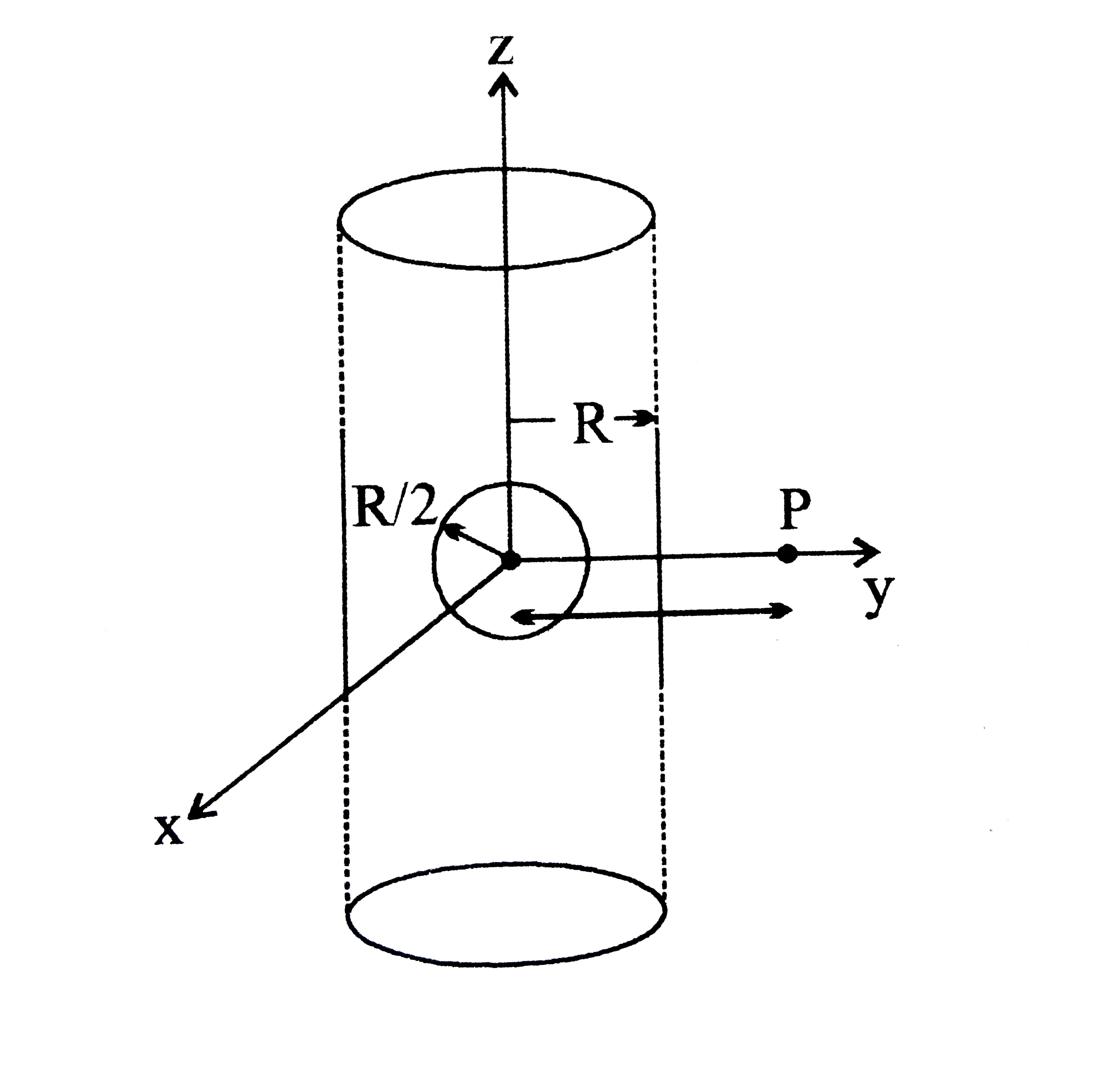 .
.
View Solution
