_S01_027_Q01.png)
If the law of gravitation be such that the force of attraction between two particles vary inversely as the 5/2th power of their separation then the graph of orbital velocity v0 plotted against the distance r of a satellite from the earth's centre on a log-log scale is shown alongside the slope on a line will be
−34
−32
−1
−52
The correct Answer is:A
For m closer to M
GMm9l2−Gm2l2=ma......(1)
and of the other m
Gm2l2+GMm16l2=ma.....(2)
solving (1) and (2), we get K=7
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - ILLUSTRATION49videos
GRAVITATION
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - EVALUATE YOURSELF -13videos
GRAVITATION
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL-V54videos
GRAVITATION
- BOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I6videos
FRICTION
- BOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)52videos
KINETIC THEORY OF GASES
Similar Questions
The energy density u is plotted against the distance r from the centre of a spherical charge distribution on a log-log scale. Find the magnitude of slope of obtained straight line.
View SolutionThe force of attraction (A) between two objects, whose masses are fixed, varies inversely with the square of their distance of separation 9d). The force of attraction between them is 2 units when the distance is 5 cm. what is the distance between the two objects, if the attraction between them is 8 units?
View Solution
Knowledge Check
- Question 1 - Select One
_S01_027_Q01.png)
If the law of gravitation be such that the force of attraction between two particles vary inversely as the 5/2th powr of their separation then the graph of orbital velocity v0 plotted against the distance r of a satellite from the earth's centre on a log-log scale is shown alongside the slope oline will beA−54B−52C−34D−1 - Question 2 - Select One
Suppose the gravitational attraction varies inversely as the distance from the earth. The orbital velocity of a satellite in such a case varies as nth power of distance where n is equal to
A−1BzeroC+1D+2 - Question 3 - Select One
The gravitational force between two objects is proportional to 1/R (and not as 1/R2) where R is separation between them, then a particle in circular orbit under such a force would have its orbital speed v proportional to
A1R2BR0CR1D1R
If the gravitational force had varied as r−5/2 instead of r−2,the potential energy of a particle at a distance ‘r’ from the centre of the earth would be directly proportional to
View SolutionIn last question assume that circular orbit of the satellite has radius r−(0). Find ΔVV9for which the maximum distance of the satellite from the centre of the earth become 2r0 after the rocket is fired.
View SolutionNewton's universal law of gravitation is expressed mathematically as
F=Gm1m2d2
Answer the following the question based on this law:
(i) what is represented by m1,m2 and d?
(ii) what is G called?
(iii) what is the meaning of the world 'universal' in this law?
(iv) Gravitational force between any two ordinary objects is really weak. why?
(v) why you or your friend sitting near you do not move towards each other due to gravitation force of attraction?
(vi) Though gravitational force is the weakest force in nature, yet it is responsible for holding our solar system.why?
(vii) will gravitational force of attraction between two bodies change when they are placed same distance apart (i) on earth (ii) on moon?
(viii) how will gravitational force change between two bodies when distance between them is halved?
(ix) masses of each of two bodies are doubled. how should the distance between them be changed to keep the gravitational force constant?View SolutionA: If the force of gravitation in inversely proportional to the distance r rather than r2 given by Newton , then orbital velocity of the satellite around the earth is independent of r .
R : GMmr=mv2r so , v=√GM hence independent of r .View SolutionA solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be
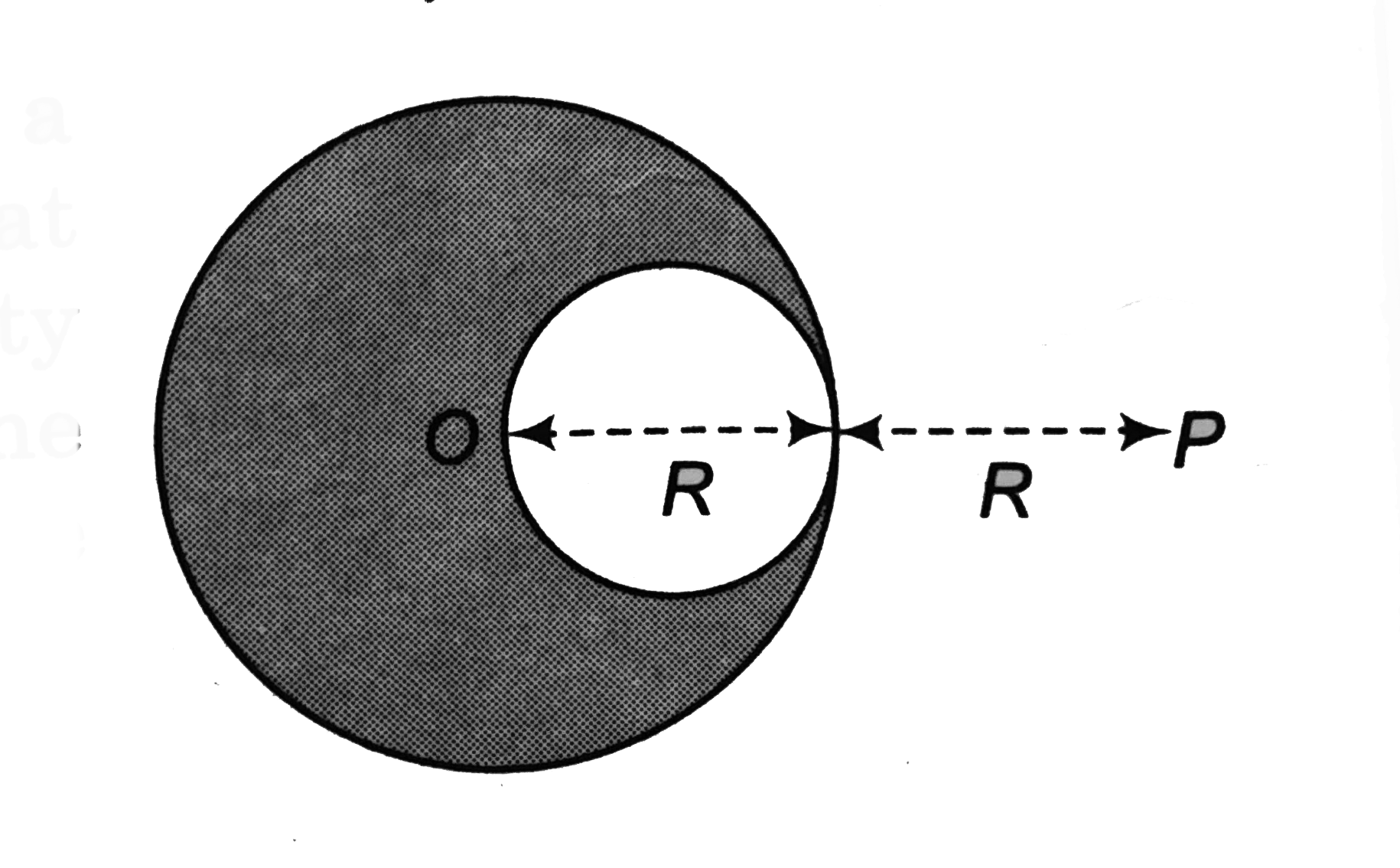 View Solution
View Solution

