P is the centre of the circle prove that ∠XPZ=2(∠XZY+∠YXZ)
Step by step video & image solution for P is the centre of the circle prove that /_XPZ =2(/_XZY+/_YXZ) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
Two tangent segments PA and PB are drawn to a circle with centre O such that ∠APB=120∘ . Prove that OP=2 AP .
View SolutionIn Figure, PA and PB are tangents from an external point P to a circle with centre O . LN touches the circle at M . Prove that PL+LM=PN+MN .
View SolutionIn Figure, O is the centre of a circle and PO BISECTS ∠APD. Prove that AB=CD
View SolutionIn the figure, P is the centre of the circle. Prove that: ∠XPZ=2 (∠XZY+ ∠YXZ)
View SolutionPoint O is the centre of a circle . Line a and line b are
parallel tangents to the circle at P and Q. Prove that
segment PQ is a diameter of the circle.

View SolutionFor the four circles M, N, O and P, following four equations are given :
Circle M : x2+y2=1
Circle N : x2+y2–2x=0
Circle 0 : x2+y2−2x−2y+1=0
Circle P : x2+y2–2y=0
If the centre of circle M is joined with centre of the circle N, further centre of circle N is joined with centre of the circle O, centre of circle O is joined with the centre of circle P and lastly, centre of circle P is joined with centre of circle M, then these lines form the sides of a :
View SolutionIn the figure, O is the centre of both the circles. AB and AC touch the small circle at P and Q.A,B and C are points on the large circle.
Prove that Ab=AC.
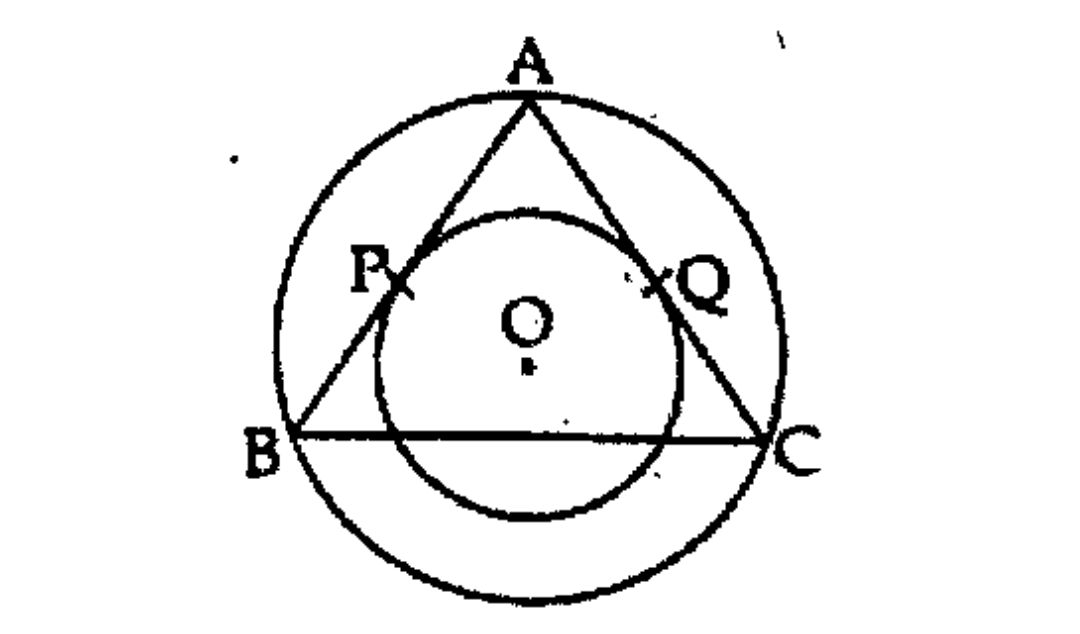 .
.
View SolutionThe equal chords AB and CD of circle with centre O, when produced, meet at P outside the circle. Prove that :
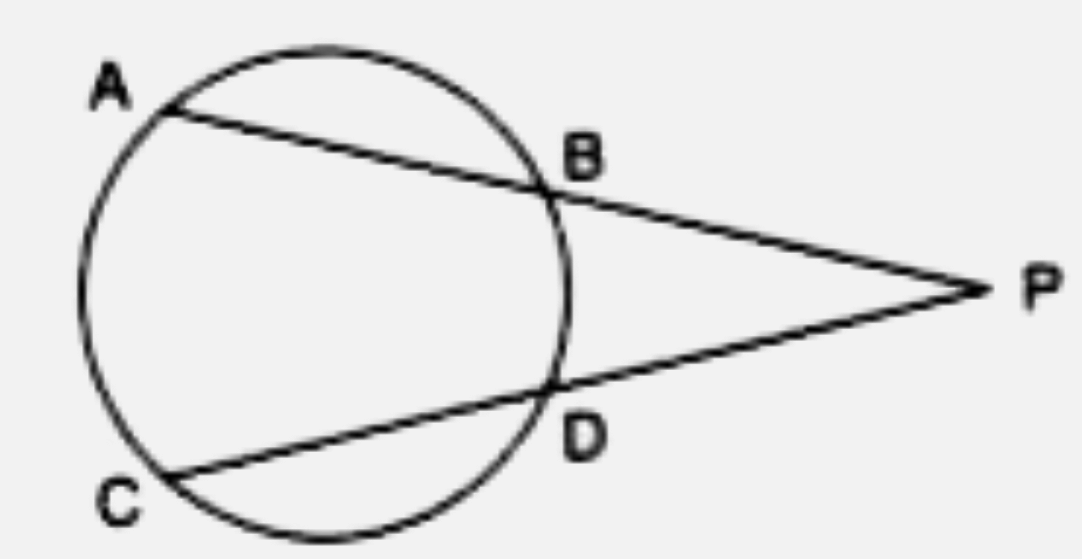
PB=PD
View Solution
