A particle is projected from origin with speed u. Find the minimum value of u if the particle passes through a poiny P(a,√3a).
Let θ be an angle of projection. The equation of trajectory of projectile
y=xtanθ−gx22u2cos2θ
2u2y=2u2xtanθ−gx2sec2θ
2u2√3a=2u2atanθ−ga2(1tan2θ)
ga2tan2θ−2u2atanθ+(ga2+2u2√3a)=0
if the particle passes through P, for this tanθ should be real, for tanθ to be real, discriminant
[(−2u2a)2−4ga2(ga2+2√3u2a)]≥0
u4−g2a2−2√3u2ga≥0
u4−2√3u2ga+3g2a2≥(g2a2+3g2a2)
(u2−√3ga2)≥(2ga)2
u2−√3ga≥2ga
u≥√(2+√3)ga
umin=√(2+√3)ga
OR
y=xtanθ−gx22u2cos2θ
√3a=atanθ−ga2sec2θ2u2 (i)
2√3u2a=2au2tanθ=−ga2sec2θ
For u to be minimum dudθ=0
2√3a.2ududθ=2a[2ududθtanθ+u2sec2θ]
−ga22secθ.secθtanθ=0
0=2au2sec2θ−2ga2sec2θtanθ
=u2−gatanθ⇒tanθ=u2ga in (i)
√3a=atanθ=−ga22u2(1+tan2θ)
=a.u2ga−ga22u2(1+u4g2a2)
Solving u=√(2+√3)ga
Topper's Solved these Questions
Similar Questions
A particle is projected from origin at an angle is selected as X-axis and verticle as Y-axis . It is found that particle passes through the points (a, b) and (b, a). Calculate range and angle of projection .
View SolutionA particle is projected from the origin in such a way that it passes through a given point P (a, b} What is the minimum requrired speed to do so?
View Solution
Knowledge Check
- Question 1 - Select One or More
A particle is projected vertically upwards in vacuum with a speed u.
AWhen it rises to half its maximum height, its speed becomes u/2.BWhen it rises to half its maximum height, its speed becomes u/√2.CThe time taken to rise to half its maximum height is half the time taken to reach its maximum height.DThe time taken to rise to three− fourth of its maximum height is half the time taken to reach its maximum height. - Question 2 - Select One
A point particle of mass 0.5 kg is moving along the x-axis under a force described by the potential energy V shown below. It is projected towards the right from the origin with a speed v. What is the minimum value of v for which the particle will escape infinitely fasr away from the origin ?
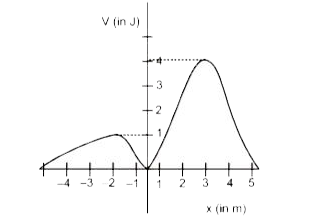 A2√2ms−1B2ms−1C4ms−1DThe particle will never escape
A2√2ms−1B2ms−1C4ms−1DThe particle will never escape - Question 3 - Select One or More
A particle is projected at an angle θ from ground with speed u (g = 10 m/s2 )
Aif u = 10 m/s and θ=30∘, then time of flight will be 1 secBIf u=10√3m/sandθ=60∘, then time of flight will be 3 sec.Cif u=10√3m/sandθ=60∘, then after 2 sec velocity becomes perpendicular to initial velocity.Dif u = 10 m/s and θ=30∘, then velocity never becomes perpendicular to initial velocity during its flight.
In a region, potential energy varies with X as U(x)=30−(x−5)2 Joule, where x is in meters. A particle of mass 0.5 kg is projected from x=11 m towards origin with a velocity 'u' . u is the minimum velocity, so that the particle can reach the origin. (x=0). find the value of u/2 in meter/second. (Take √44=6.5)
View SolutionA particle of mass m is projected from origin O with speed u at an angle θ with positive x-axis. Positive y-axis is in vertically upward. Direction. Find the angular momentum of particle at any time t about O before the particle strkes the ground again.
View SolutionA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .View Solution
.View Solution
A particle is projected from surface of the inclined plane with speed u and at an angle θ with the horizontal. After some time the particle collides elastically with the smooth fixed inclined plane for the first time and subsequently moves in vertical direction. Starting from projection, find the time taken by the particle to reach maximum height. (Neglect time of collision).View SolutionFigure shows that particle A is projected from point P with velocity u along the plane and simultaneously another particle B with velocity v at an angle α with vertical. The particles collide at point Q on the plane. Then
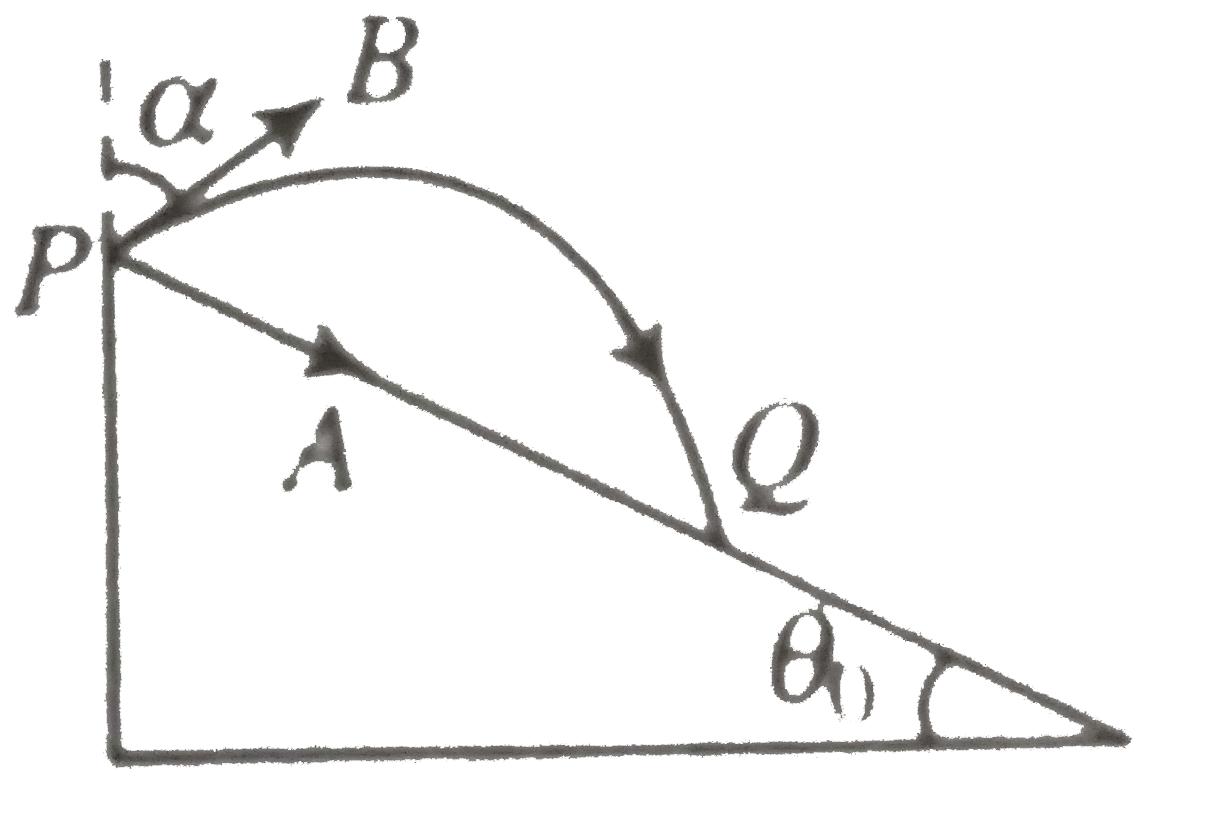 View Solution
View Solution

