A particle is projected from the origin in such a way that it passes through a given point P (a, b} What is the minimum requrired speed to do so?
Step by step video & image solution for A particle is projected from the origin in such a way that it passes through a given point P (a, b} What is the minimum requrired speed to do so? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Level-186videos
DESCRIPTION OF MOTION
- BOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Level-225videos
DESCRIPTION OF MOTION
- BOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Level-334videos
DESCRIPTION OF MOTION
- BOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Matching type13videos
FORCE ANALYSIS
Similar Questions
A particle is projected from origin with speed u. Find the minimum value of u if the particle passes through a poiny P(a,√3a).
View SolutionA particle is projected from a point O with an initial speed of 30ms−1 to pass through a point which is 40m from O horizontally and 10m above O. There are two angles of projection for which this is possible. These angles are α and β. The value of |tan(α+β)| is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle is projected with an angle of projection θ to the horizontal line passing through the points (P,Q) and (Q,P) referred to horizontal and vertical axes (can be treated as X-axis and Y-axis respectively). The angle of projection can be given by
Atan−1[P2+PQ+Q2PQ]Btan−1[P2+Q2−PQPQ]Ctan−1[P2+Q22PQ]Dsin−1[P2+Q2+PQ2PQ] - Question 2 - Select One
With what minimum speed must a particle be projected from origin so that it is able to pass through a given point (30m,40m) ? Take g=10m/s2
A60m/sB30m/sC50m/sD40m/s - Question 3 - Select One
Equations of the line passing through the origin and the point (a,b,c) are
Ax−ax−0=y−by−0=z−cz−0Bx−aa=y−bb=z−ccCx−ab−c=y−bc−a=z−ca−bDa(x−a)=b(y−b)=c(z−c)
A ball is projected vertically up such that it passes thorugh a fixes point after a time t0 and t2 respectively. Find
a. The height at which the point is located with respect to the point of projeciton
b. The speed of projection of the ball.
c. The velocity the ball at the time of passing through point P.
d. (i) The maximum height reached by the balll relative to the point of projection A (ii) maximum height reached by the ball relative to point P under consideration.
e. The average speed and average velocity of the ball during the motion from A to P for the time t1 and t2 respectively.
 .View Solution
.View SolutionA particle is projected from point A perpendicular to inclined plane with a velocity 50m/s as shown in the figure. Particle strikes a vertical plane perpendicularly at point B. Time taken by particle in going from point A to point B is
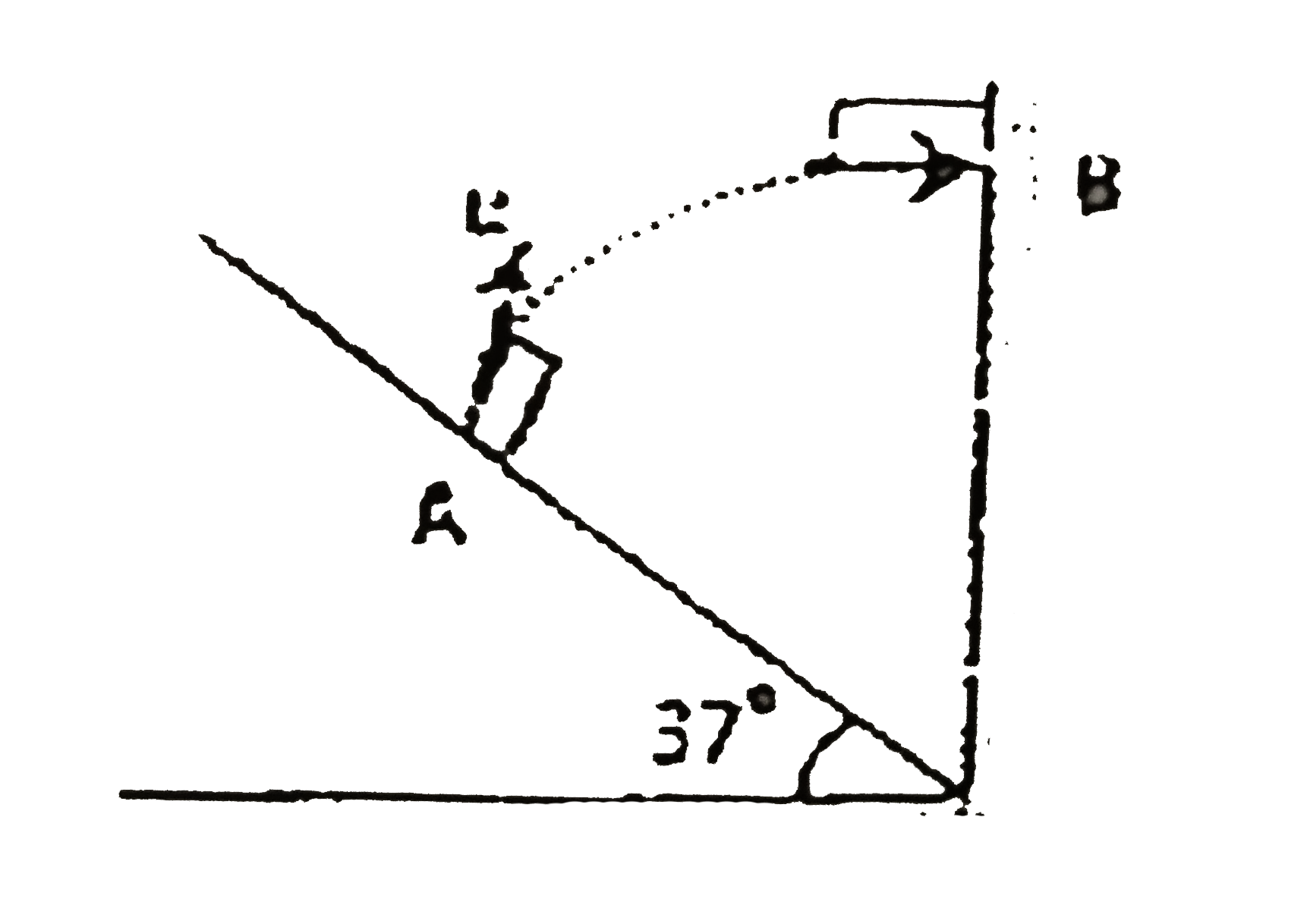 View Solution
View SolutionA particle is projected from origin at an angle is selected as X-axis and verticle as Y-axis . It is found that particle passes through the points (a, b) and (b, a). Calculate range and angle of projection .
View SolutionA particle projected atv a definite angle ∝ to the horizontal passes through points (a,b)and(b,a), referred to horizontal and vertical axes through the points of projection. Show that :
(a) The horizontal range R=a2+ab+b2a+b .
(b) The angle of projection ∝ is given by
tan−1[a2+ab+b2ab].View SolutionA particle is projected from the ground with an initial speed of v at an angle θ with horizontal. The average velocity of the particle between its point of projection and highest point of trajectroy is :
View Solution

