A block of mass 2 kg is resting on a smooth surface. At what angle a force of 10 N be acting on the block so that it will acquire a kinetic energy of 10 J after moving 2 m
30∘
45∘
60∘
90∘
The correct Answer is:C
To solve the problem step by step, we will use the work-energy theorem, which states that the work done on an object is equal to the change in its kinetic energy.
Step 1: Understand the Given Data
- Mass of the block (m) = 2 kg
- Force applied (F) = 10 N
- Distance moved (d) = 2 m
- Final kinetic energy (KE_final) = 10 J
- Initial kinetic energy (KE_initial) = 0 J (since the block is at rest)
Step 2: Apply the Work-Energy Theorem
According to the work-energy theorem:
Work done=ΔKE=KEfinal−KEinitial
Substituting the values:
Work done=10J−0J=10J
Step 3: Calculate the Work Done by the Applied Force
The work done by the applied force can be expressed as:
Work done=F⋅d⋅cos(θ)
Where:
- F is the force applied (10 N)
- d is the distance moved (2 m)
- θ is the angle between the force and the direction of displacement
Substituting the known values:
10J=10N⋅2m⋅cos(θ)
Step 4: Simplify the Equation
10J=20N⋅m⋅cos(θ)
Dividing both sides by 20:
cos(θ)=10J20N⋅m=12
Step 5: Find the Angle
The cosine of the angle is given by:
cos(θ)=12
This corresponds to:
θ=60∘
Final Answer
The angle at which the force of 10 N should be applied to achieve a kinetic energy of 10 J after moving 2 m is 60 degrees.
---
- Mass of the block (m) = 2 kg
- Force applied (F) = 10 N
- Distance moved (d) = 2 m
- Final kinetic energy (KE_final) = 10 J
- Initial kinetic energy (KE_initial) = 0 J (since the block is at rest)
According to the work-energy theorem:
Work done=ΔKE=KEfinal−KEinitial
Substituting the values:
Work done=10J−0J=10J
The work done by the applied force can be expressed as:
Work done=F⋅d⋅cos(θ)
Where:
- F is the force applied (10 N)
- d is the distance moved (2 m)
- θ is the angle between the force and the direction of displacement
10J=10N⋅2m⋅cos(θ)
10J=20N⋅m⋅cos(θ)
Dividing both sides by 20:
cos(θ)=10J20N⋅m=12
The cosine of the angle is given by:
cos(θ)=12
This corresponds to:
θ=60∘
The angle at which the force of 10 N should be applied to achieve a kinetic energy of 10 J after moving 2 m is 60 degrees.
Topper's Solved these Questions
Similar Questions
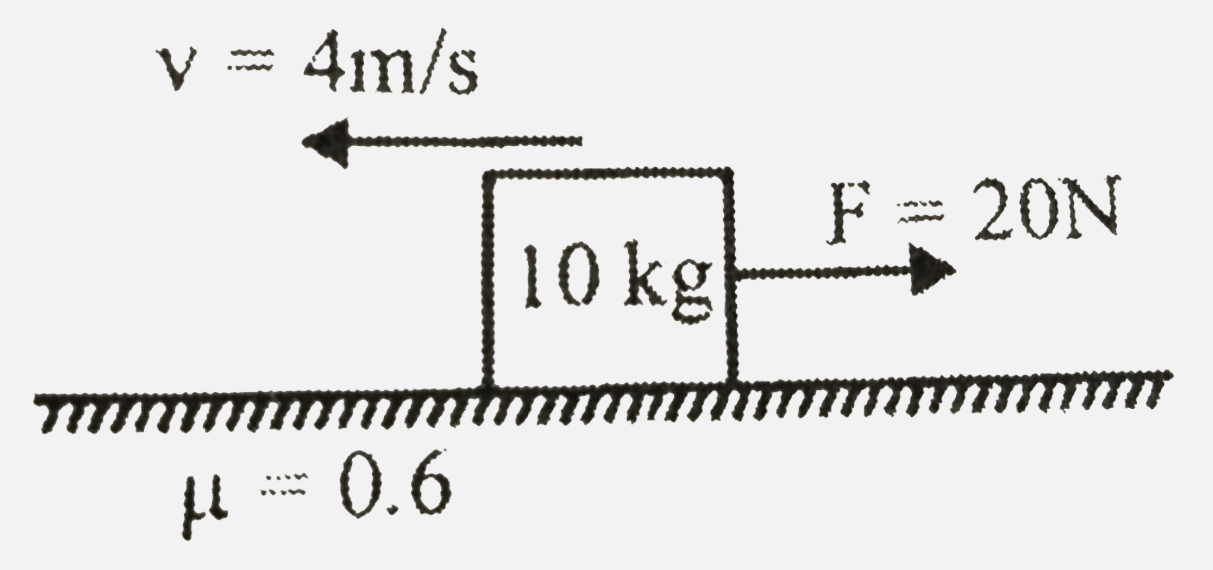
A block of mass 10 kg is moving on a rough surface as shown in figure. The frictional force acting on block is :-
View SolutionA block of mass 2kg is sliding on a smooth surface. At t=0, its speed is v0=2m/s. At t=0, a time varying force starts acting on the block in the direction opposite to v0 if the speed of object is 38Nm/s at t=10s. Find the value of N

View Solution
Knowledge Check
A block of mass 5 kg is resting on a smooth surface. At what angle a force of 20 N be acted on the body so that it will acquired a kinetic energy of 40 J after moving 4 m?
A30∘B45∘C60∘D120∘A block of mass 5 kg is resting on a smooth surface at what angle a force of 20 N be acted on the body so that it will acquire a kinetic energy of 40 J after moving 4 m?
A300B450C600D1200A force of 75 N is applied to a block of mass 25 kg, resting on a smooth horizontal surface. In how much time, the block will acquire a speed of 12 m/s?
A1 secB2secC4 secD8 sec
A block of mass 10kg is placed on a horizontal surface as shown in the figure and a force F=100N is applied on the block as shown, in the figure. The block is at rest with respect to ground. If the contact force between block and ground is 25n (in Newton) then value of n is : (Takeg=10m/s2)

View SolutionA block of mass 5kg rests on a rough horizontal surface. It is found that a force of 10N is required to make the block just move However , once the motion begains, a force of only 8N is enough to maintain the motion find the coefficient of kinetic and static friction between the block and the horizontal surface

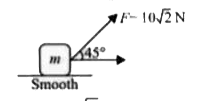
View SolutionA block of mass 20 kg is moving on a smooth surface by pulling through a light string of tension 10√2 N. Find the work done by string on the block for a displacement of 2 m along the surface.
View SolutionA block of mass, 2 kg is kept on a smooth surface as shown. It is being applied by a force F=20ˆi+10ˆj Find the displacement of the block in 10 seconds.
View SolutionA block is kept on a rough horizontal surface. A variable horizontal force is acting on the block as shown in the figure. At t=0, block is at rest. Kinectic energy of block at t=5sec will be (g=10m/s2)
View Solution
