Three thin unifrom circular discs each of mass M and radius R are placed touching each other on a horizontal surface such that an equilateral triangle is formed, when the center of three discs are joined. Find the M.I. about an axis passing through the center of mass system of discs and perpendicular to the plane.
The center of mass of system is at O (due to symmetry)
Distance between the center of mass of system O and the center of disc d=2R/√3 (side of equilateral triangle is 2R)
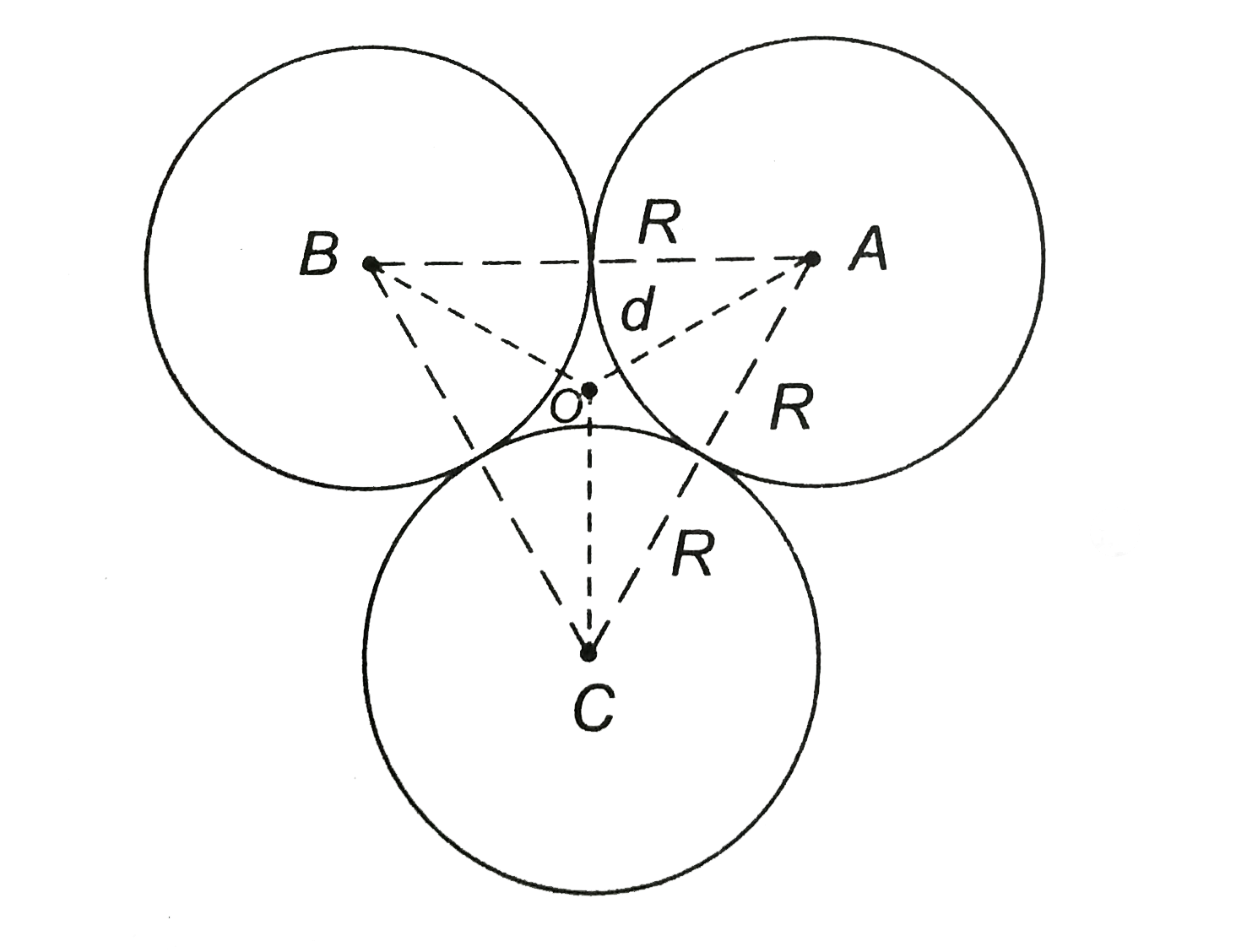
M.I. of disc about its own axis =12MR2
M.I. of disc about O
I1=12MR2+Md2=12MR2+M(2R√3)2
=11MR26
I0=3I1=33MR26
Topper's Solved these Questions
Similar Questions
Three thin, uniform, indentical rods each or mass M and length L are joined as shown. Find the M.I. about an axis passing through O and perpendicular to the plane.
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View Solution
Knowledge Check
- Question 1 - Select One
Three identical metal balls each of radius r are placed touching each other on a horizontal surface such that an equilateral triangle is formed, when the center of three balls are joined. The center of mass of system is located at the
Ahorizontal surfaceBcenter one of the ballsCline joining centers of any two ballsDpoint of intersection of medians - Question 2 - Select One
Three identical metal balls, each of the radius r are placed touching each other on a horizontal surface such that an equilateral triangle is formed when centres of three balls are joined. The centre ofthe mass of the system is located at
Aline joining centres of any two ballsBcentre of one of the ballsChorizontal surfaceDhorizontal surface - Question 3 - Select One
The M.I. of disc of mass M and radius 'R' about an axis passing through midway between centre and circumference and perpendicular to its plane is
AMR2/2B5/4MR2CMR2D3/4MR2
Calculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
View SolutionFrom a disc of radius r1, a concentric disc of radius r2 is removed . The mass of the remaining portion is m. Find the M.I. of the remaining about an axis passing through the center of mass and perpendicular to the plane.
View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passig through its centre of mass and perpendicular to the plane of the particle.View SolutionThree discs each of mass M and radius R are placed in contact with each other as shown in figure here. Then the MI of the system about an axis XX' is
 View Solution
View SolutionThe radius of gyration of a uniform disc of radius R, about an axis passing through a point R2 away from the centre of disc, and perpendicular to the plane of disc is:
View Solution

