The moment of inertia of thin square plate ABCD of uniform thickness about an axis passing through the center O and perpendicular to the plane of the plate is
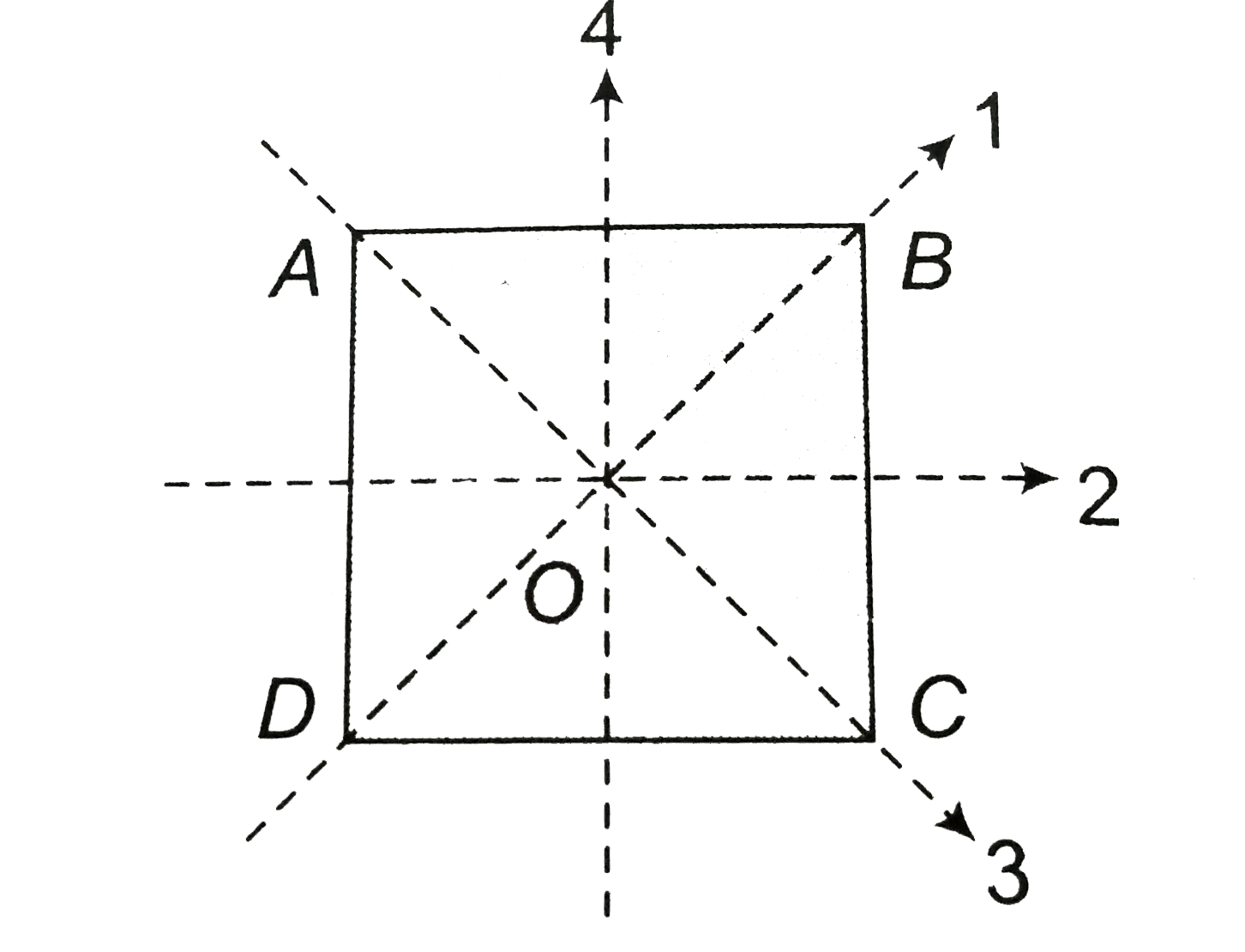
(i) I1+I2
(ii) I2+I4
(iii) I1+I3
(iv) I1+I2+I3+I4
where I1, I2, I3 and I4 are repectively moments of inertia about axes 1, 2, 3 and 4 which are in the plane of the plane
(i),(ii)
(i), (ii), (iii)
(ii), (iii)
(i), (iii)
As explained in the previous problem
I1=I2=I3=I4
I0=I1+I2=I2+I4 (⊥ar axes theorem)
=I1+I3
Topper's Solved these Questions
Similar Questions
If I1,I2 ,and I3 are moments of inertia of a disc about its geometric axis,diameter and a tangent in its plane,then
View SolutionThe moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is I0. What is the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod ?
View Solution
Knowledge Check
The moment of inertia of a thin square plate ABCD of uniform thickness about an axis passing through the centre O and perpendicular to the plane of the plate is
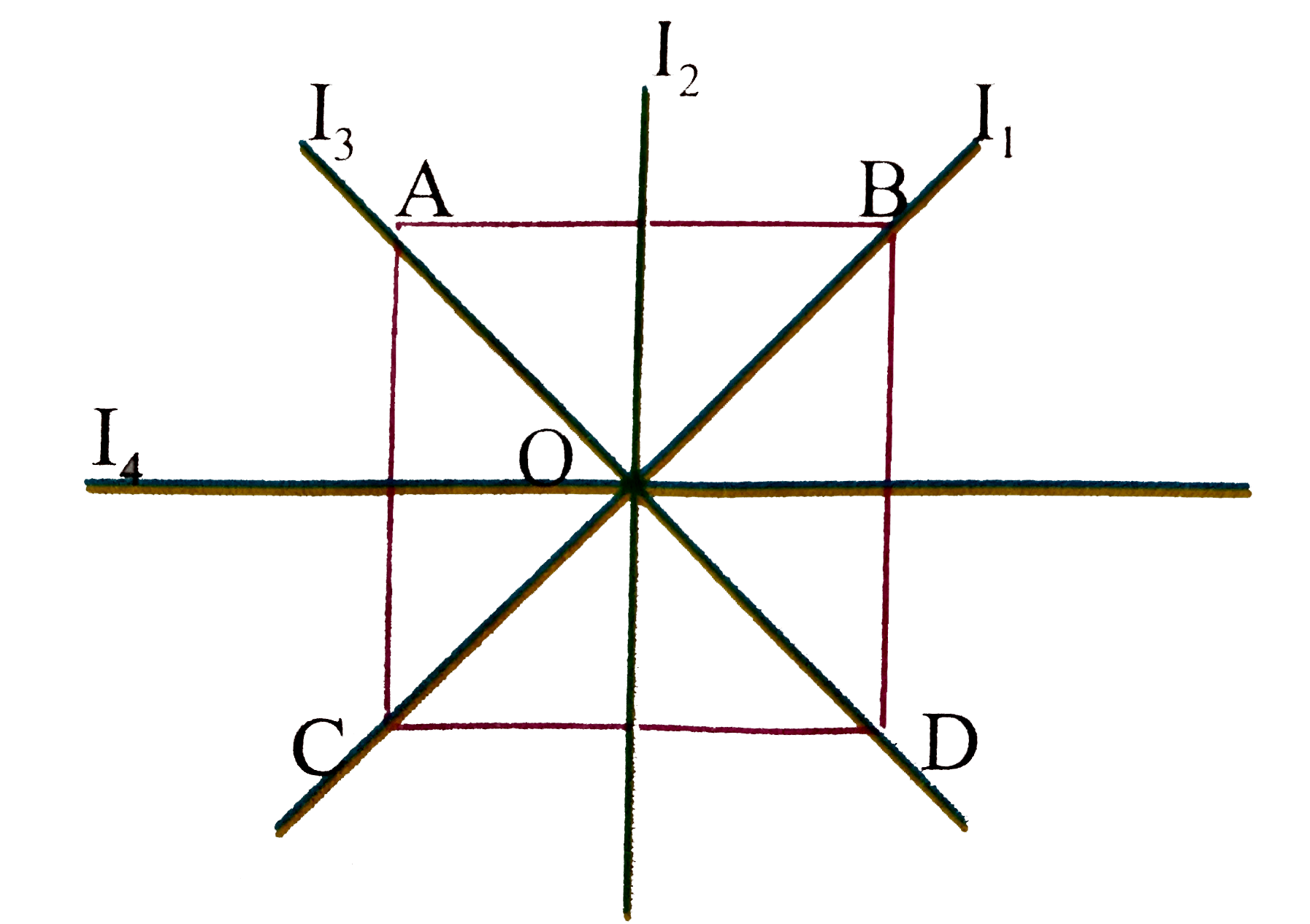
(a)I1+I2, (b)I2+I4
2I1+I3, (d) I1+2I3Aa,b are trueBb,c are trueCc,d are trueDb,d are trueThe moment of inertia of a thin square plate ABCD, fig, of uniform thickness about an axis passing through the centre O and perpendicular to the plane of the plate is
where l1,l2,l3andl4 are respectively the moments of intertial about axis 1,2,3 and 4 which are in the plane of the plate.
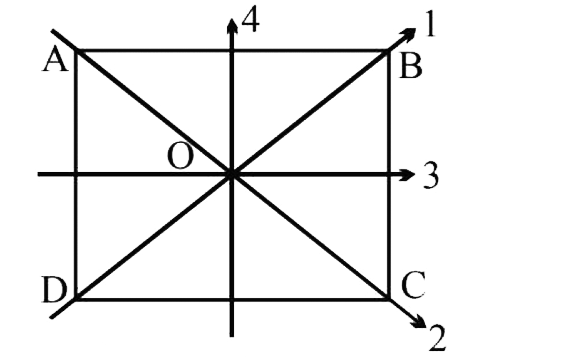 Al1+l2Bl3+l4Cl1+l3Dl1+l2+l3+l4
Al1+l2Bl3+l4Cl1+l3Dl1+l2+l3+l4Moment of inertia of a rectangular plate about an axis passing through P and perpendicular to the plate is I. Moment of PQR about an axis perpendicular to the plane of the plate :
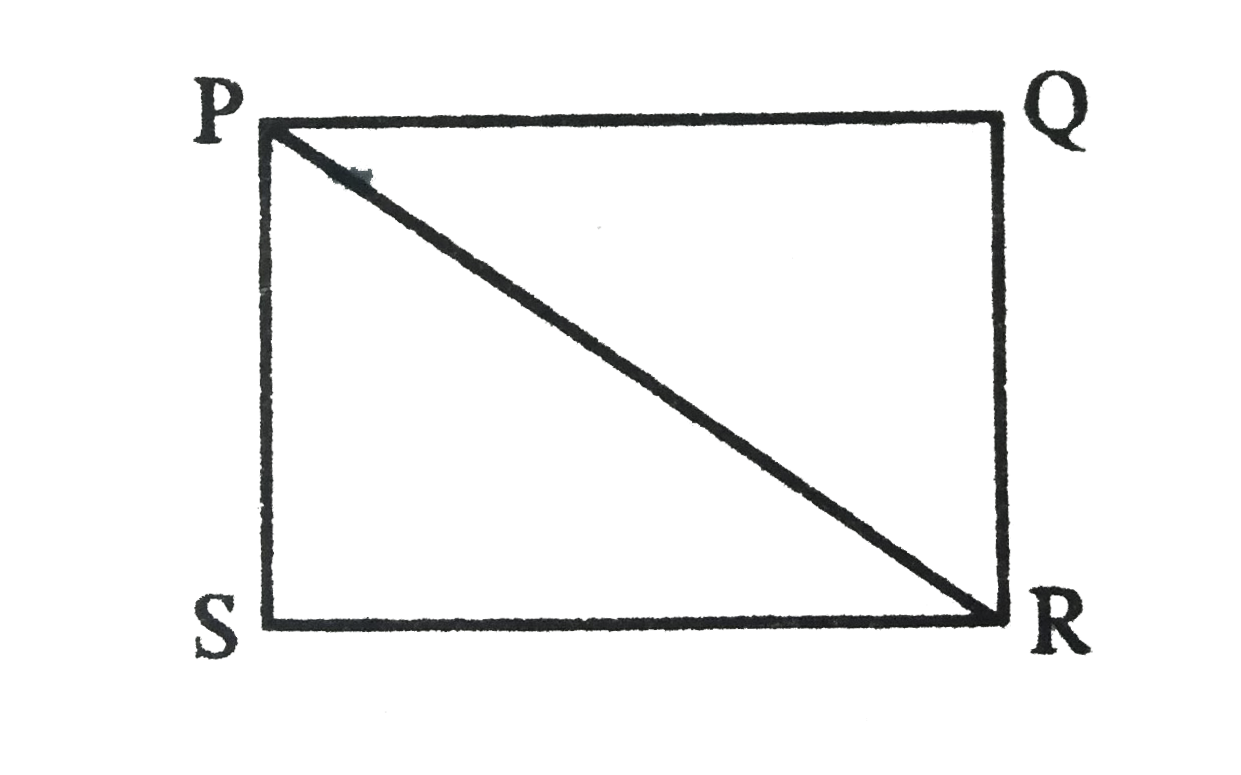 .Aabout P=I/2Babout R=I/2Cabout P>I/2Dabout R>I/2
.Aabout P=I/2Babout R=I/2Cabout P>I/2Dabout R>I/2
I is moment of inertia of a thin square plate about an axis passing through opposite corners of plate. The moment of inertia of same plate about an axis perpendicular to the plane of plate and passing through its centre is
View SolutionThe moment of inertia of a uniform thin rod of mass m and length L about two axis PQ and RS passing through centre of rod C and in the plane of the rod are IPQ and IRS respectively. Then IPQ+IRS is equal to
View SolutionThe moment of inertia of a uniform thin rod of mass m and length l about two axis PQ and RS passing through centre of rod C and in the plane of the rod are IPQ and IRS respectivley. Then IPQ+IRS is equal to.
 .
.
View SolutionThe moment of inertia of a uniform rod about a perpendicular axis passing through one end is I1. The same rod is bent into a ring and its moment of inertia about a diameter is I2. Then I1/I2 is
View SolutionMoment of inertia of uniform triangular plate about axis passing through sides AB,AC,BC are Ip,IB and IH respectively and about an axis perpendicular to the plane and passing through point C is IC. Then :
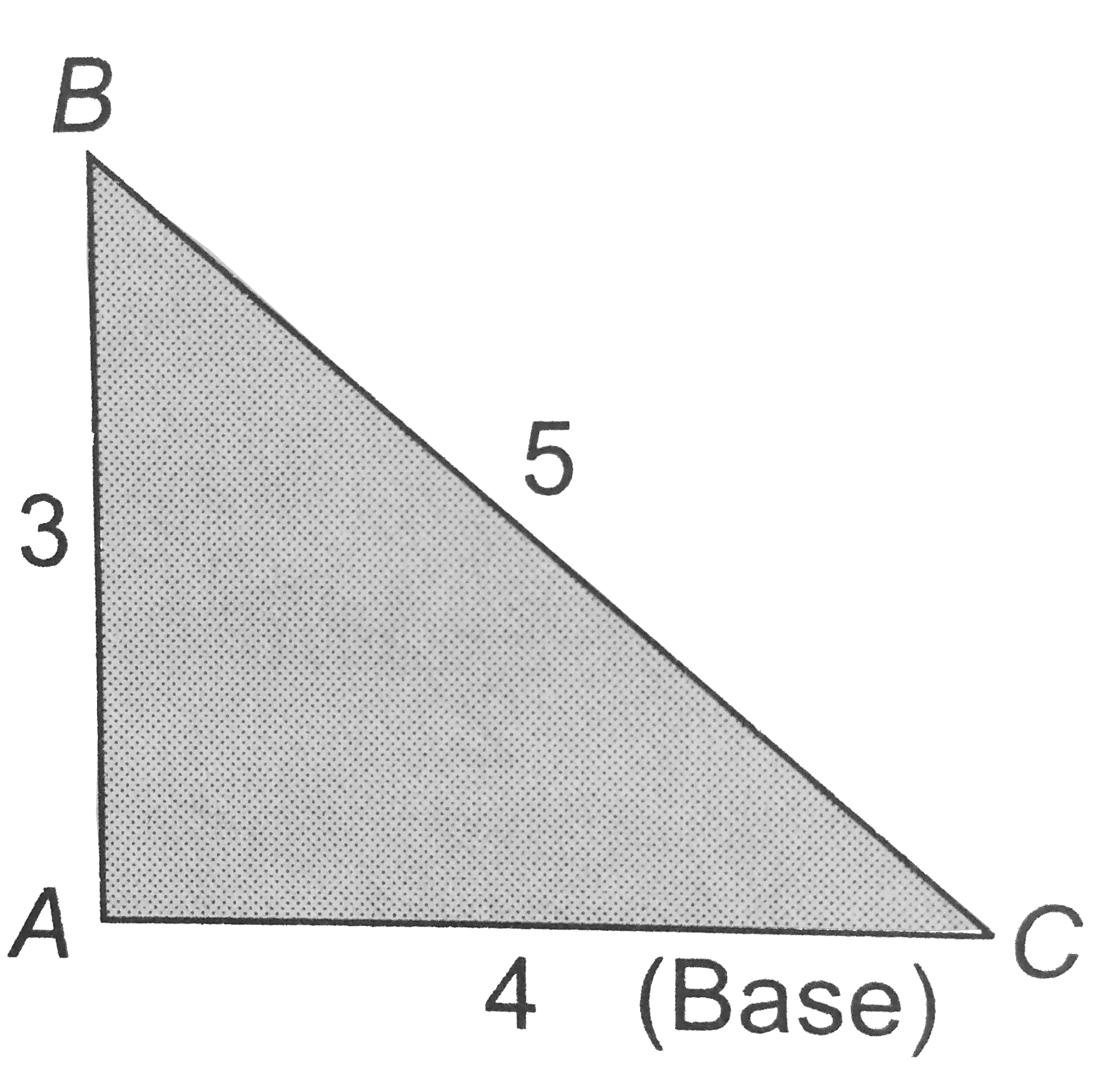 .
.
View Solution
