Let I be the moment of interia of a uniform square plate about an axis AB that passses through its centre and is parallel to two its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle θ with AB. The moment of inertia of the plate about the axis CD is then equal to-
I
Isin2θ
Icos2θ
Icos2(θ2)
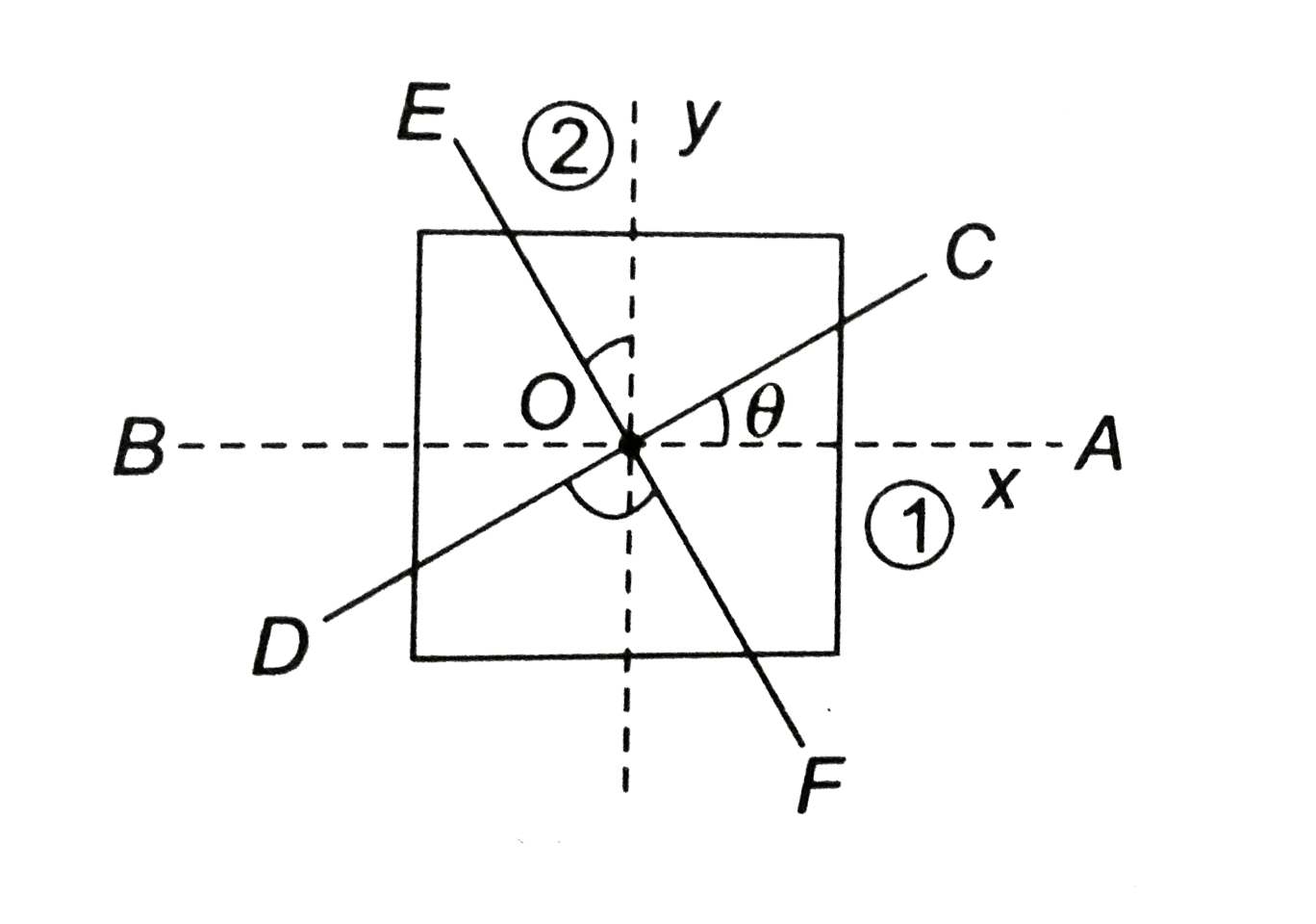
For the square plate, I1=I2=ma212=I
For an axis passing through the center O and ⊥ar to the plane
I1+I2=Iz (⊥ar axes theorem)
CD and EF are ⊥ar
ICD+IEF=Iz
By summetry ICD=IEF=I1=I2=I
In fact, M.I. about any axis passing through O (center) and lying in the plane of plane =ma212=I
Topper's Solved these Questions
Similar Questions
The moment of inertia of a square plate of mass 4kg and side 1m about an axis passing through its centre and perpendicular to its plane is
View SolutionThe moment of inertia of uniform rectangular plate about an axis passing through its mid-point and parallel to its length l is (b = breadth of rectangular plate)
View Solution
Knowledge Check
Let I be the moment of interia of a uniform square plate about an axis AB that passses through its centre and is parallel to two its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle θ with AB. The moment of inertia of the plate about the axis CD is then equal to-
AlBlsin2θClcos2θDlcos2θ2The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
Aincreases if its temperature is increasedBchanges if its axis of rotation is changedCincreases if its angular velocity is increasedDboth (a) and (b) are correctMoment of inertia of a circular ring about an axis through its centre and perpendicular to its plane is
AI=12MR2BI=MR2CI=32MR2DI=52MR2
The moment of inertia of a uniform square plate of mass M and edge length a about one of its diagonals is
View SolutionThe moment of inertia of a thin uniform rod of mass M, length L, about an axis passing through its centre and making an angle θ with the rod is
View SolutionThe moment of inertia of a thin square plate ABCD of uniform thickness about an axis passing through its center and perpendicular to its plane will
View SolutionFind the moment of inertia of a uniform square plate of mass M and edge a about one of its diagonals.
View SolutionThe moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an angle α is
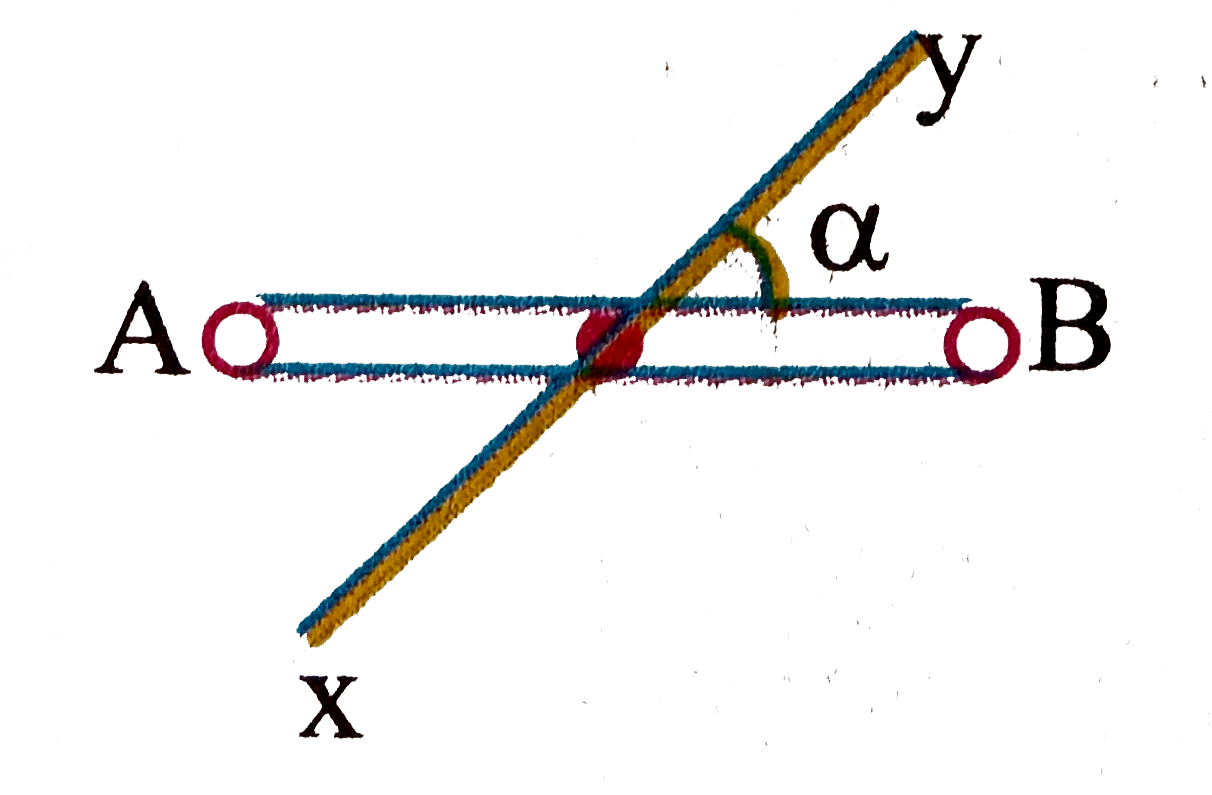
View Solution
