Find the equillibrium length for the system after increasing temperature by $Δ T$ .

Video Solution

Text Solution

Verified by Experts

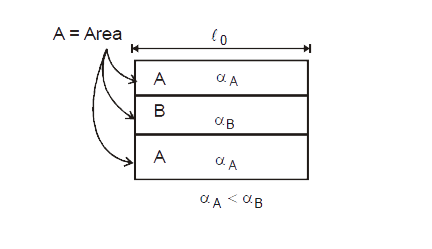
here $l_{A} and l_{B}$ are the natural length of the rod A and B after increase in temperature by $Δ T, and l_{0}$ is actual length after temperature increase by $Δ T$ .
So strain in A $= \frac{l'_{0} - l'_{A}}{l'_{A}}$

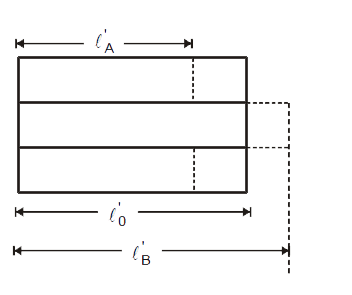
and in $B = \frac{l'_{B} - l'_{0}}{l'_{B}}$
Now force balance
Now $\frac{F}{A} = γ_{A} = \frac{l'_{0} - l'_{A}}{l'_{A}} ...(1)$
and $\frac{2 F}{A} = γ_{B} \frac{l'_{B} - l'_{0}}{l'_{B}} ....(2)$

(1) ÷ (2)
$\frac{1}{2} = \frac{γ_{A}}{γ_{B}} \frac{[l'_{0} - l'_{0} (1 + α_{A} Δ T)] l_{0} (1 + α_{B} Δ T)}{l_{0} (1 + α_{A} Δ T) [l_{0} (1 + α_{B} Δ T) - l'_{0}]}$
$l'_{0} = \frac{l_{0} (γ_{B} + 2 γ_{A}) [1 + (α_{B} + α_{A}) Δ T)}{2 l_{A} (1 + α_{B} Δ T) + γ_{B} (1 + α_{A} Δ T)}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELASTICITY AND THERMAL EXPANSION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The temperature of the system increases during an
Aisothermal expansion
Badiabatic compression
Cadiabatic expansion
Disothermal compression
Question 2 - Select One
The coefficient of linear expansion varies linearly from $α_{1}$ and $α_{2}$ in a rod of length $l$ . Find the increase in length when its temperature is increased by $Δ T$ .
A $(\frac{α_{1} + α_{2}}{2}) l Δ T$
B $(α_{1} + α_{2}) l Δ T$
C $(α_{1} + \frac{α_{2}}{2}) l Δ T$
D $(\frac{α_{1}}{2} + α_{2}) l Δ T$
Question 3 - Select One
Consider the following statements
I. In general, the temperature dependence of the equilibrium constant depends on the sign of $Δ H$ for the reaction.
II. The equilibrium constant for an exothermic reaction (negative $Δ H$ ) decreases as the temperature increases.
III. The equilibrium constant for an endothermic reaction (positive $Δ H$ ) increases as the temperature increases.
Choose the correct statement(s).
AI and II
BOnly II
CII and III
DAll of these

MOTION-ELASTICITY AND THERMAL EXPANSION-Exercise - 4 (Level-II)

Home
Ask Doubt
Profile